Façamos com que o arco da Terra entre Alexandria e Siene seja chamado arco AS, e que toda a circunferência da Terra seja chamada arco CE.
Deixe o ângulo no centro da Terra ser chamado ângulo a e os 360° completos do círculo sejam chamados ângulo b.
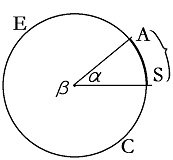
Por Euclides III-27, temos
arco EC / arco AS = ângulo b / ângulo a
Por hipótese, o comprimento do arco AS é de 5.000 estádios e o ângulo a é igual a 1/50 de um círculo.
Como o ângulo b é a medida do ângulo de um círculo completo, ângulo b = 1 círculo.
Substituindo esses valores numéricos reais pela razão anterior, obtemos:
arco EC / arco AS = ângulo b / ângulo a
arco EC / 5000 estádios = 1 / (1/50)
arco CE = 5000 estádios / (1/50)
arco CE = 250000 estádios.
Portanto, como o comprimento do arco EC é igual à circunferência da Terra, obtemos que a circunferência da Terra é de aproximadamente 250.000 estádios.
Índice
- Eratóstenes e o mistério dos estádios – Introdução
- Eratóstenes e o mistério dos estádios – O problema básico
- Eratóstenes e o mistério dos estádios – Meridiano de Alexandria e Siena
- Eratóstenes e o mistério dos estádios – Raios de luz paralelos
- Eratóstenes e o mistério dos estádios – Distância entre Alexandria e Siena
- Eratóstenes e o mistério dos estádios – O ângulo entre a sombra e a haste em Alexandria
- Eratóstenes e o mistério dos estádios – A Terra é esférica
- Eratóstenes e o mistério dos estádios – Argumentos de Eratóstenes – I
- Eratóstenes e o mistério dos estádios – Argumentos de Eratóstenes – II
- Eratóstenes e o mistério dos estádios – Argumentos de Eratóstenes – III
- Eratóstenes e o mistério dos estádios – Quanto mede um estádio?
- Eratóstenes e o mistério dos estádios – A correção de Eratóstenes
- Eratóstenes e o mistério dos estádios – Conclusão
