Eratóstenes e o mistério dos estádios – Argumentos de Eratóstenes – II

MrBiTs

Por Euclides I-29, uma linha reta que cai em linhas retas paralelas torna os ângulos alternados iguais entre si.

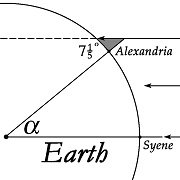
Chamemos o ângulo no centro da Terra de a.

Por hipótese, o ângulo formado pela sombra em Alexandria é igual a 1/50 de um círculo. Portanto, a medida desse ângulo é 360° / 50 = 7 1/5°.

Por Euclides I-29, como o ângulo em Alexandria e o ângulo a são ângulos internos alternados, a medida do ângulo a também é de 360° / 50 = 7 1/5°.

Por Euclides III-27, em círculos iguais, os ângulos em circunferências iguais são iguais.

Algumas explicações ajudarão a revelar como Euclides III-27 é usado nesse argumento.

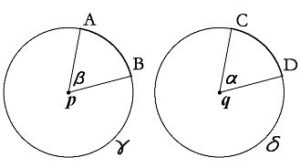
Dados dois círculos iguais g e d, com centros p e q respectivamente, se o arco AB é igual ao arco CD, então o ângulo b é igual ao ângulo a.

Como todo círculo é igual a si mesmo, pela quarta noção comum de Euclides, podemos aplicar essa proposição a um único círculo.

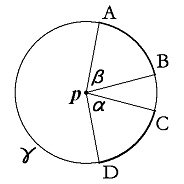
Dado o círculo g, com o centro p, se o arco AB for igual ao arco CD, o ângulo b será igual ao ângulo a.

Como valores numéricos reais, eles podem ser colocados na forma de razão:

arco CD / arco AB = ângulo a / ângulo b

Usando esta forma de proporção, Eratóstenes agora usará três valores conhecidos para resolver o quarto valor desconhecido – a circunferência da Terra.

Índice

  1. Eratóstenes e o mistério dos estádios – Introdução
  2. Eratóstenes e o mistério dos estádios – O problema básico
  3. Eratóstenes e o mistério dos estádios – Meridiano de Alexandria e Siena
  4. Eratóstenes e o mistério dos estádios – Raios de luz paralelos
  5. Eratóstenes e o mistério dos estádios – Distância entre Alexandria e Siena
  6. Eratóstenes e o mistério dos estádios – O ângulo entre a sombra e a haste em Alexandria
  7. Eratóstenes e o mistério dos estádios – A Terra é esférica
  8. Eratóstenes e o mistério dos estádios – Argumentos de Eratóstenes – I
  9. Eratóstenes e o mistério dos estádios – Argumentos de Eratóstenes – II
  10. Eratóstenes e o mistério dos estádios – Argumentos de Eratóstenes – III
  11. Eratóstenes e o mistério dos estádios – Quanto mede um estádio?
  12. Eratóstenes e o mistério dos estádios – A correção de Eratóstenes
  13. Eratóstenes e o mistério dos estádios – Conclusão