O teste consistiu em medir a distância entre a base e o topo de dois edifícios distantes entre si cerca de 3.000 km, um em Natal (RN) e outro em Torres (RS).
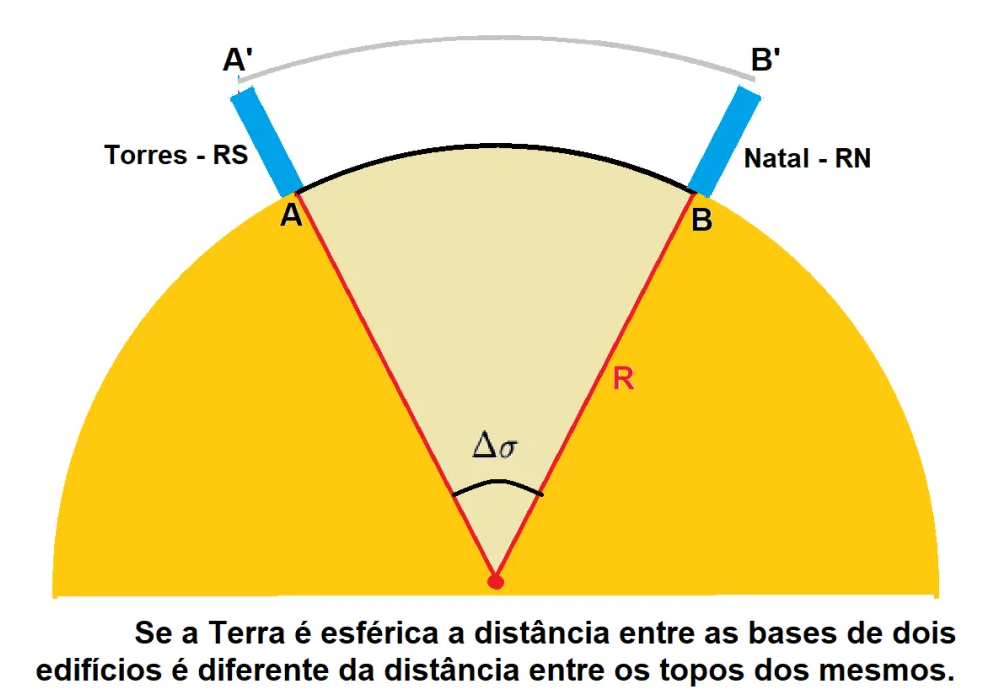
Como foi efetuado o teste?
Quem responde é o Prof. Antonio Vieira:
Para efetuar tal medida seria necessário que, no mínimo, 4 satélites GPS fossem rastreados simultaneamente pelas duas estações separadas 3.000 km.
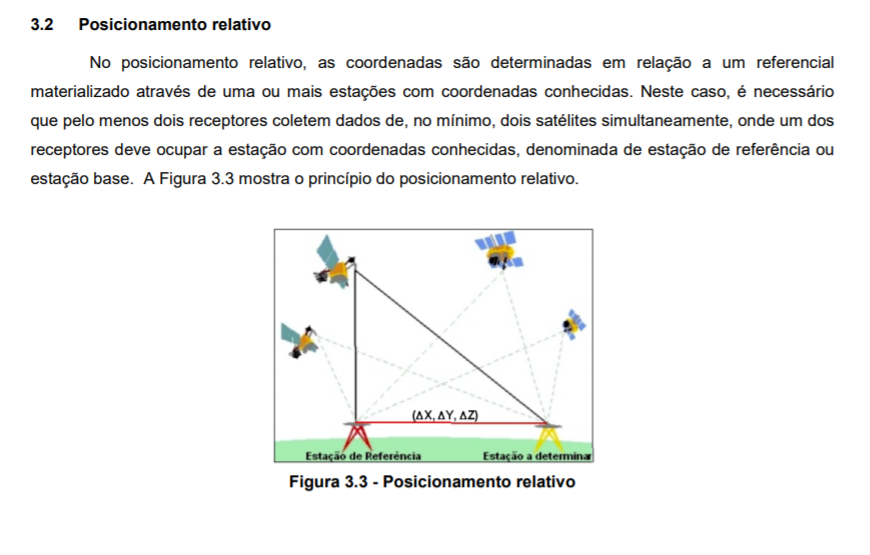
Como a arquitetura das órbitas não permite isso. mesmo supondo que fosse possível, os sinais sofreriam influência da ionosfera, acarretando erros nas duas distâncias deduzidas (topo e base).

Ao determinar as coordenadas de um ponto próximo ao edifício em Natal. provavelmente usaram como referência um vértice da RBMC, do IBGE, formando um pequeno triângulo onde um dos vértices foi o ponto GPS, calculou-se o triângulo e transportou-se as coordenadas GPS para a base e para o topo do edifício, repetindo este processo em Torres.
Com as coordenadas (X, Y, Z) referentes ao elipsóide WGS -84 (referencial geométrico do GPS), calculou os vetores entre as bases e os topos do prédio. (É provável que isto tenha sido feito pelo software).
Este procedimento não surte resultados efetivos uma vez que QUALQUER medição está submetida a erros de precisão, desvio padrão e propagação de erros.

Na distância medida com rastreadores GPS ocorre erro relativo de 1/100.000 da distância medida. (este valor é alcançado quando se formam circuitos).
Mesmo considerando que a medida tenha essa precisão, a distância do vértice da RBMC até ao vértice perto do prédio deve ser da ordem de 100 m = 100.000 m. logo, 1/100.000 × esta distância contém um erro de 1 metro.
Soma-se também os erros do transporte das coordenadas para o topo e a base do prédio.
Portanto, mesmo que a distância nominal, calculada com as coordenadas X,Y,Z, sejam iguais a incerteza entre elas é maior do que 1 metro.
Sendo assim, na distância de aproximadamente 3000 km, o erro acumulado seria enorme, mesmo se fosse possível rastrear, SIMULTANEAMENTE, os satélites GPS.
O uso do GPS na determinação de altitudes ortométricas.
Definição de uma superfície geoidal local através de posicionamento por GPS
Determinações altimétricas empregando GPS
Qual o resultado do teste dos edifícios?
Quem reponde é o Prof. Carlos Lima:
Para determinar a altitude em tempo real com a utilização de GPS tipo RTK (Tempo Real Cinemático), utiliza-se uma segunda antena que funciona como Base Estática de Correção (base que necessita de tempo de rastreio para se determinar sua coordenada), essa base corrige a antena (Rover) que é utilizada pelo operador, obtendo assim coordenadas UTM e Altitude em tempo real. No caso do teste em questão, o equipamento utilizado é pós-processado, onde faz-se o rastreio (por algumas horas), e com o arquivo bruto das antena (RINEX) calcula-se em qualquer programa de pós-processamento, utilizando, no caso do Brasil, as bases RBMC para a obtenção das coordenadas e altitude ortométrica do ponto.
No link abaixo um estudo da “Revista Novo Tempo” onde é comparado um Nivelamento Geométrico Convencional com um levantamento com RTK:
http://sitionovo.ifto.edu.br/index.php/sitionovo/article/download/210/94
Por falta de informações, não sabemos se ocorreu o pós-processamento dos arquivos brutos, mas o que se verifica visualmente é que utilizaram como base pontos Georreferenciados, e, com uma Estação Total, mediram as distâncias. Como a estação total trabalha num plano limitado, justamente pela influência da curvatura, e como as medidas foram próximas aos edifícios, o resultado do teste apenas mostra que tais edifícios foram bem construídos e estão aprumados.
O cálculo sugerido no experimento em questão não tem utilidade prática. As diferenças de altitude ortométrica e diferença angular sobre a curva equipotencial são utilizadas localmente ou em conjunto com outros pontos para fins específicos, onde a diferença equipotencial de nível realmente é importante, como canais de escoamento, contenções, calculo de áreas de risco em casos de enchentes, etc.
Um exemplo prático encontra-se no projeto da ponte Verrazzano-Narrows. Por conta da altura das torres (211 m) e a distância entre elas (1.298 m), a curvatura da superfície da Terra teve que ser levada em conta ao projetar a ponte – as torres são 4,275 cm mais afastados em seus topos do que em suas bases.
Efeito da curvatura da Terra nas dimensões da ponte Verrazzano-Narrows
Análise do teste
Distância entre os edifício em Torres/RS e Natal/RN : 3.021,79 km
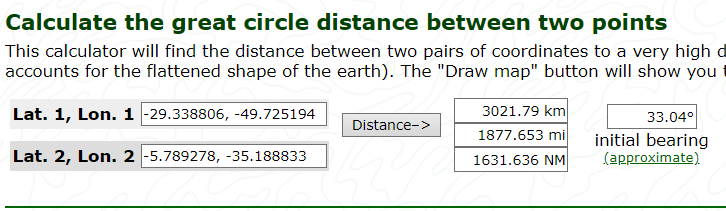
Geolocalização do edifício em Torres/RS: 29°20’19.7″S 49°43’30.7″W

https://www.emporis.com/buildings/336422/dunas-flat-service-torres-brazil
Topografia do local do edifício em Torres:
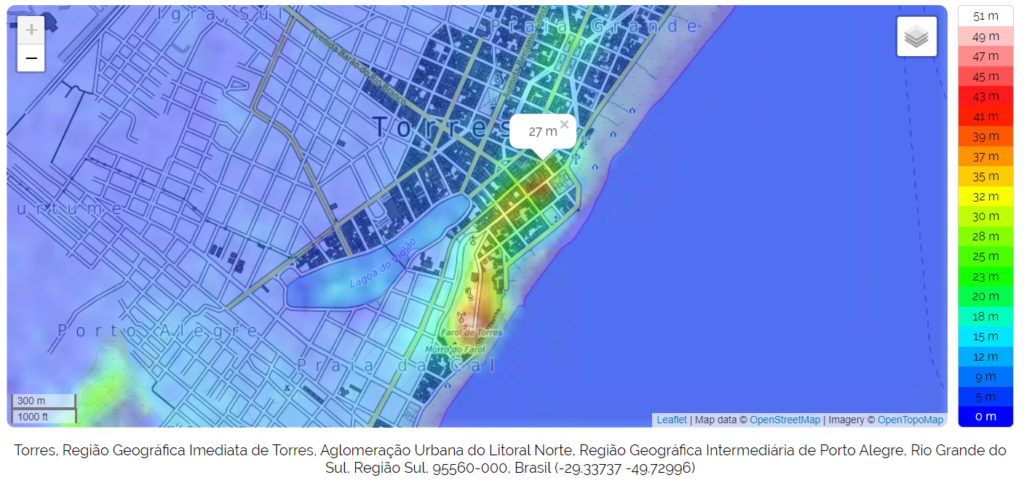
https://pt-br.topographic-map.com/maps/g2wt/Torres/
Total: 93.68 metros (68,66 m de altura mais 27 m de elevação)
Geolocalização do edifício em Natal/RN: 5°47’21.4″S 35°11’19.8″W

comparação efetuada com o edifício vizinho Oasis:
https://www.emporis.com/buildings/226385/oasis-natal-brazil
Topografia do local do edifício em Natal:
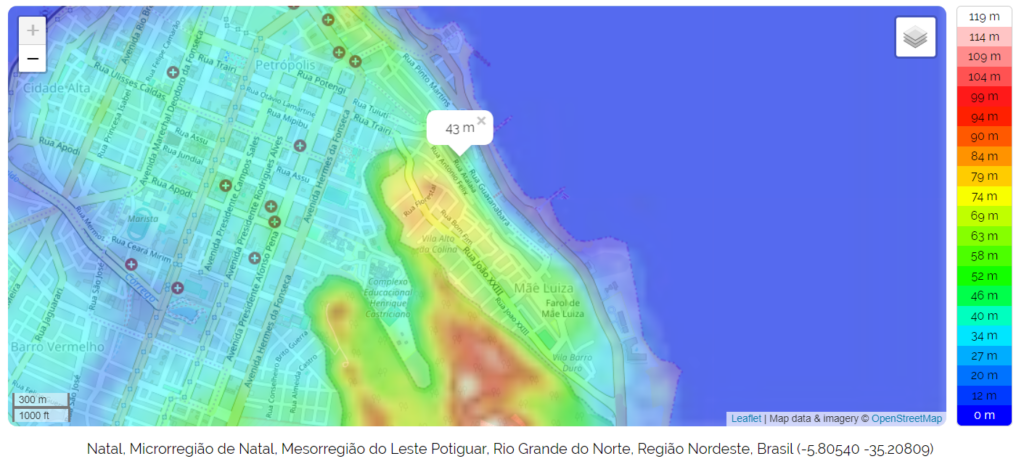
https://pt-br.topographic-map.com/maps/gn3d/Natal/
Total: 103 metros (60 m de altura mais 43 m de elevação)
Cálculo da distância entre a base e o topo dos edifícios
Para simplificação assumimos a altura de 100 metros para cada edifício.
O raio da Terra ao nível do mar em cada latitude:
Natal / -5.789278 : 6377.921 km
Torres/ -29.338806 : 6373.036 km
Raio médio: 6375.47 km (6.375.470 m)
Perímetro: 40.058,25 km (40.058.259,4 m)
Para o cálculo proposto, iniciamos com a distância geodésica entre as coordenadas: 3.021,79 km (3.021.790 m) ou distância sobre o elipsoide na malha de coordenadas.
Aplicamos a altura dos prédios ao raio médio:
6.375.470 m (raio médio da Terra) + 100 m (altura dos edifícios) = 6.375.570 m
6.375.570 m x 2 x π (3,1416) = Perímetro resultante: 40.058.887,74 m
A partir deste resultado encontramos os seguintes valores:
Comprimento de arco (acrescido da altura dos edifícios) 100 metros acima da malha geodésica: 3.021,83 km ( 3.021.837,398 m)
3.021.837,398 (arco superior) – 3.021.790 (malha geodésica)
Diferença de arco de 47,39 metros entre a base e o topo dos edifícios
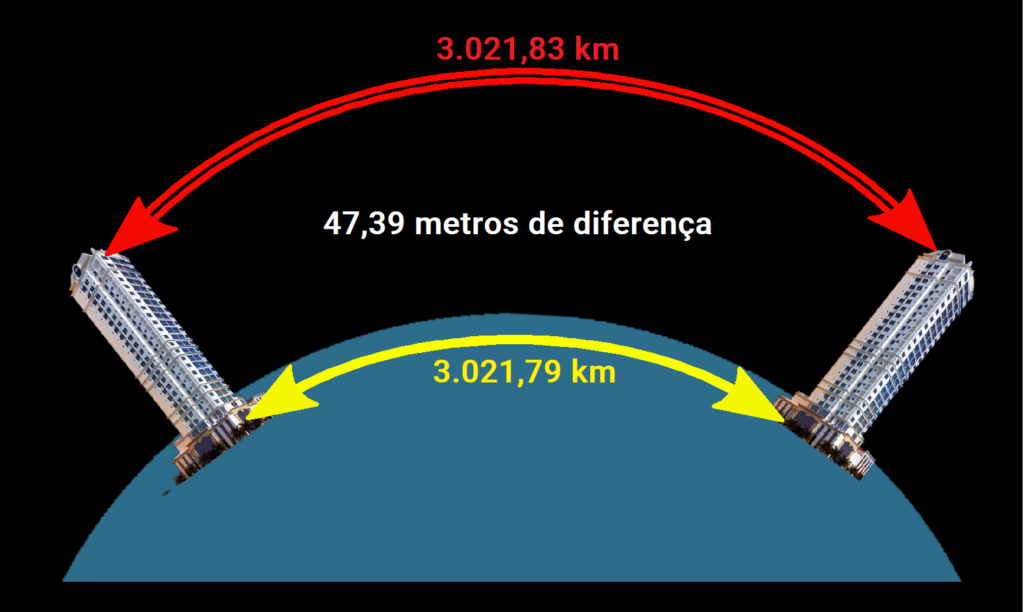
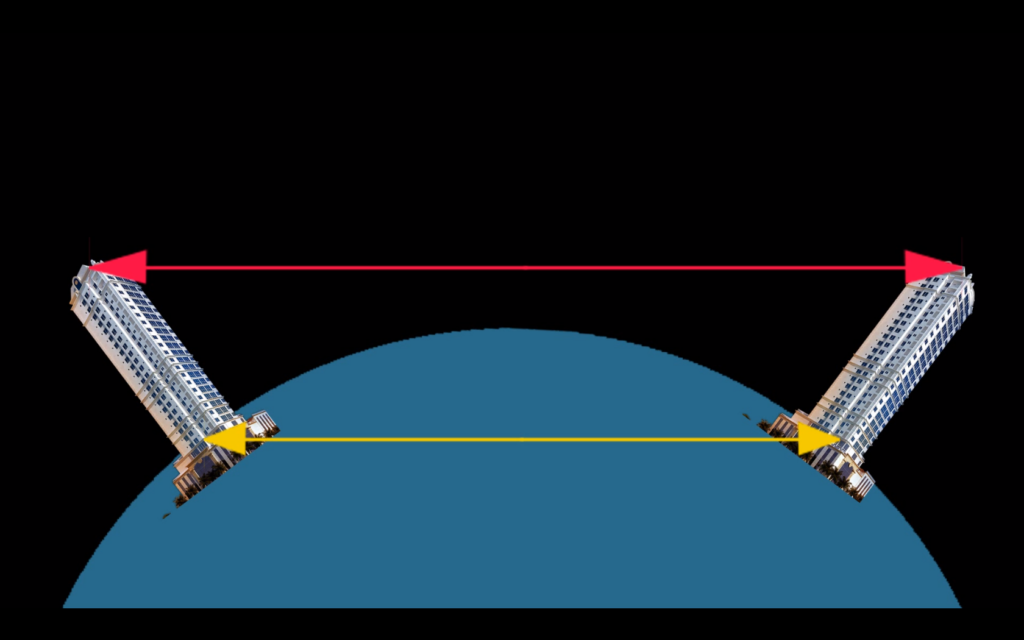
Verificando o percentual de diferença entre base e topo dos dois prédios, com o valor de ARCO temos:
47,39 m / 3.021.790 m = 0,000015682 m
Ou um percentual de 0,00157%, Q.E.D.
Mas isso não passa de uma curiosidade matemática, já que não há utilidade prática, seria como descobrir qual a distância entre dois pontos transpassando uma reta de um lado ao outro do globo terrestre.
O CREF também publicou uma análise aqui
Fontes:
https://fenix.ciencias.ulisboa.pt/downloadFile/844562369085478/levantamentos_GNSS.pdf
http://www.est-team.com/documenti/manuali/the_earth.pdf
http://www2.fct.unesp.br/docentes/carto/arana/cobrac2004.pdf
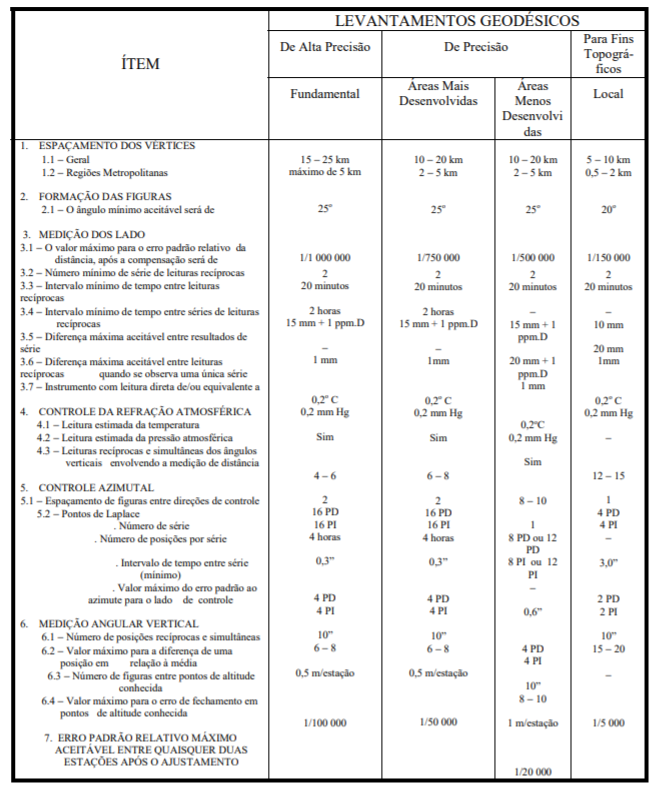
Especificações e Normas para Levantamentos Geodésicos atualizadas
http://datagenetics.com/blog/june32012/index.html
https://www.geotrackconsultoria.com.br/blog/2-metodo-relativo-de-medicoes-gps-e-gnss
https://ieeexplore.ieee.org/document/7283749
https://www.e-education.psu.edu/natureofgeoinfo/c5.html
Publicação elaborada com a valiosa ajuda do Vector, MrBits, Carlos Lima e Antonio Vieira.

