Além de Eratóstenes, outros matemáticos da antiguidade também desenvolveram formas de calcular o Raio terrestre, um dos melhores métodos foi desenvolvido pelo matemático árabe Abu Arrayhan Muhammad ibn Ahmad al-Biruni (al-Biruni) (973-1048 E.C.).

Mediante um grande problema para os matemáticos islâmicos, o problema da qibla, no qual era preciso determinar a direção exata para Meca onde uma pessoa deveria orientar-se para sua oração.

Os matemáticos islâmicos e gregos, antecessores de al-Biruni, já haviam realizado grandes progressos com o desenvolvimento da trigonometria esférica, que foi base para o método de determinação do raio terrestre, descrito por ele em suas publicações.
O método consiste na determinação do Raio terrestre medindo-se o
ângulo de declínio vertical em relação ao plano horizontal de referência, medido no alto de uma montanha com altura conhecida.
Para realizar seu método, al-Biruni precisava apenas de três elementos:
- Um astrolábio.
- Uma montanha adequada com um horizonte visível à sua frente para que o ângulo de inclinação do horizonte pudesse ser medido com precisão.
- Conhecimento de trigonometria.
A primeira etapa no método consiste em calcular a altura da montanha. Este cálculo utiliza três das quatro medidas necessárias.
As duas primeiras medidas são: o ângulo de elevação do topo de uma montanha em dois pontos diferentes em linha reta.
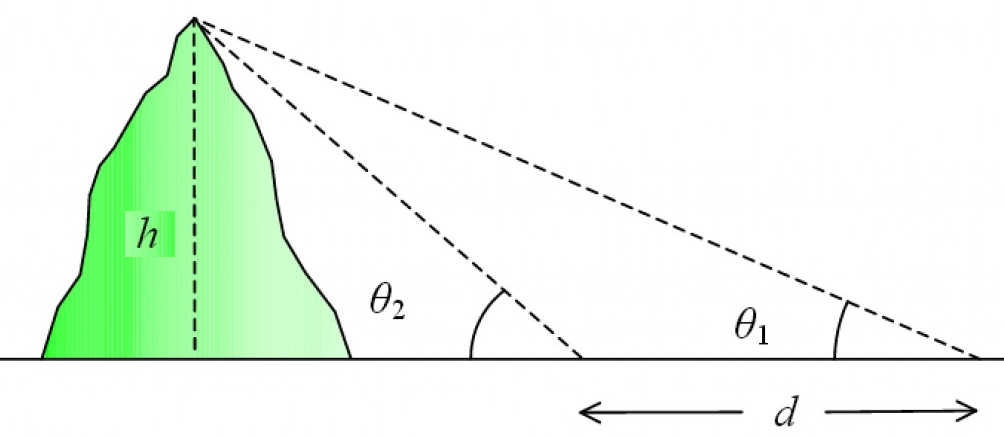
Estes foram medidos com um astrolábio. al-Biruni provavelmente tinha um astrolábio suficientemente grande para garantir a precisão máxima perto de duas casas decimais de um único grau.

A terceira medida foi a distância entre esses dois pontos. Isso talvez tenha sido encontrado usando ritmos.
A segunda etapa em seu método foi encontrar o ângulo de inclinação do horizonte a partir do topo da montanha usando o astrolábio da mesma maneira. Sendo esta a quarta medição. No diagrama abaixo nota-se que sua linha de visão do topo da montanha até o horizonte fará um ângulo de 90 ° com o raio.
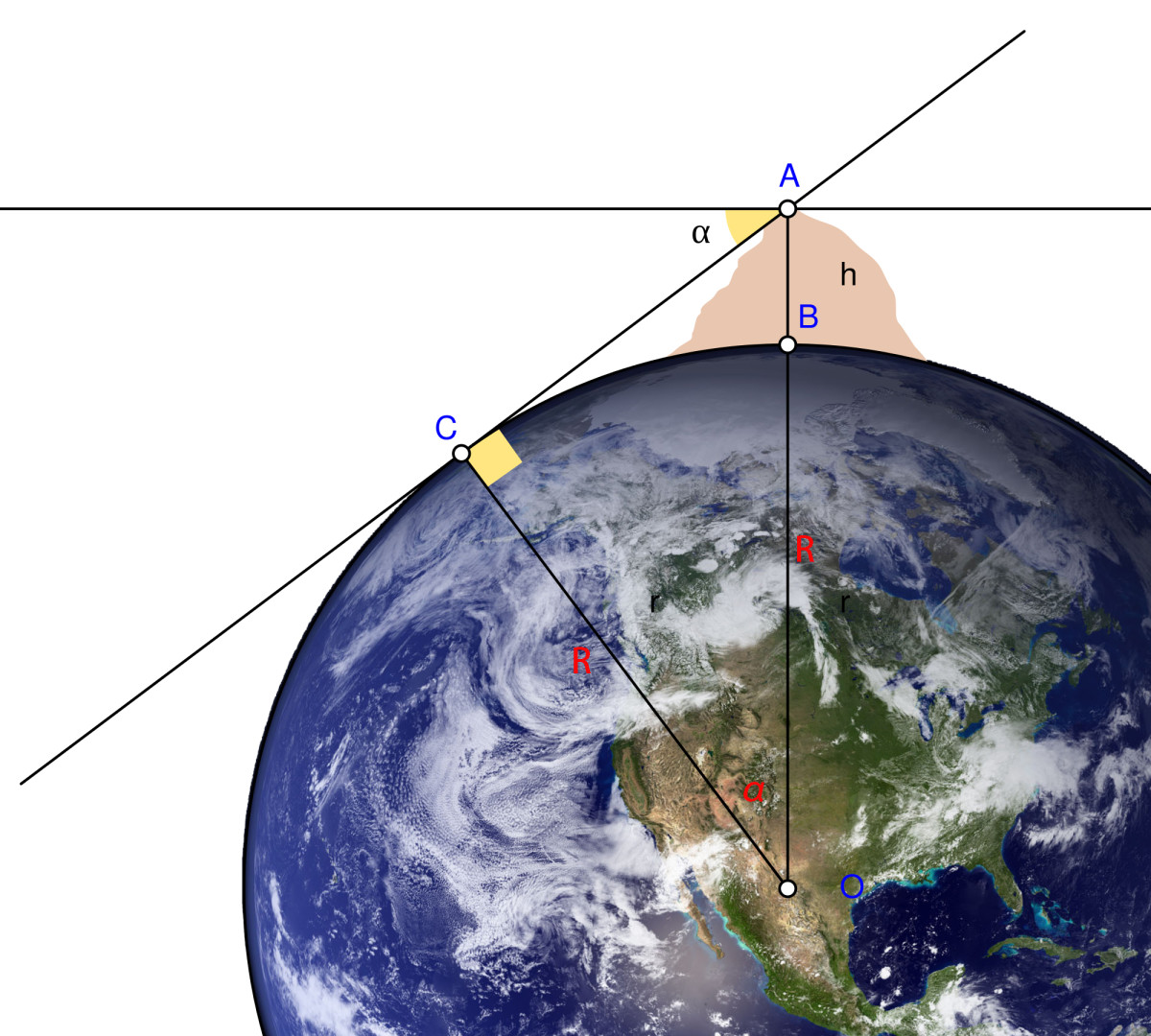
A engenhosidade desse método está em como al-Biruni descobriu que a figura que liga o centro da terra C, o topo da montanha B e o horizonte plano S era um enorme triângulo retângulo no qual a lei dos senos poderia ser feito para determinar o raio da Terra.
Dedução da Equação
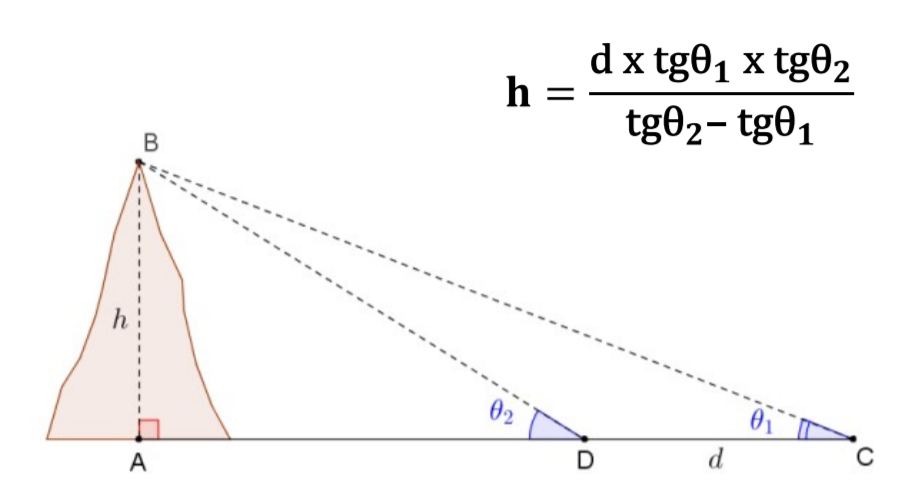
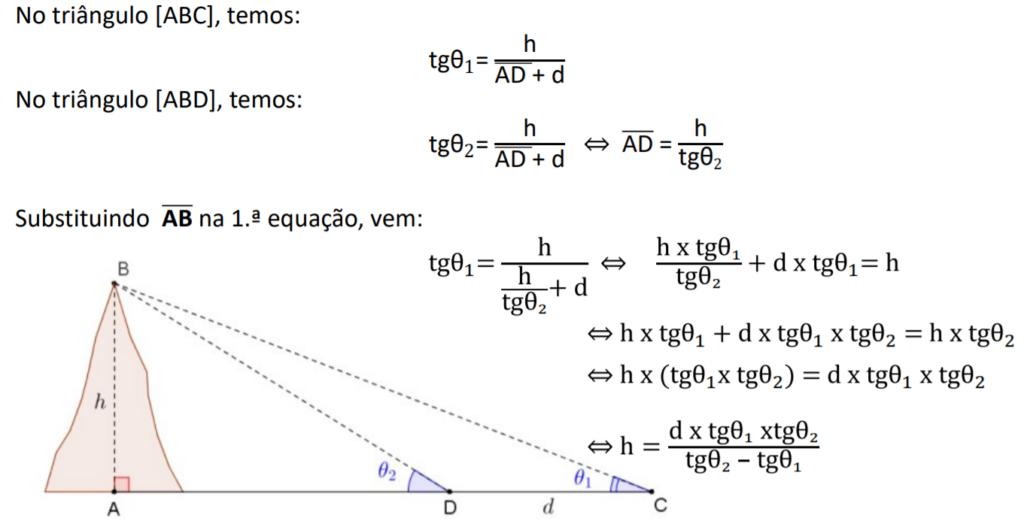
No cume de uma montanha de altura conhecida, representada pelo segmento [AB], avista-se do ponto B o horizonte ao longo da linha BT.
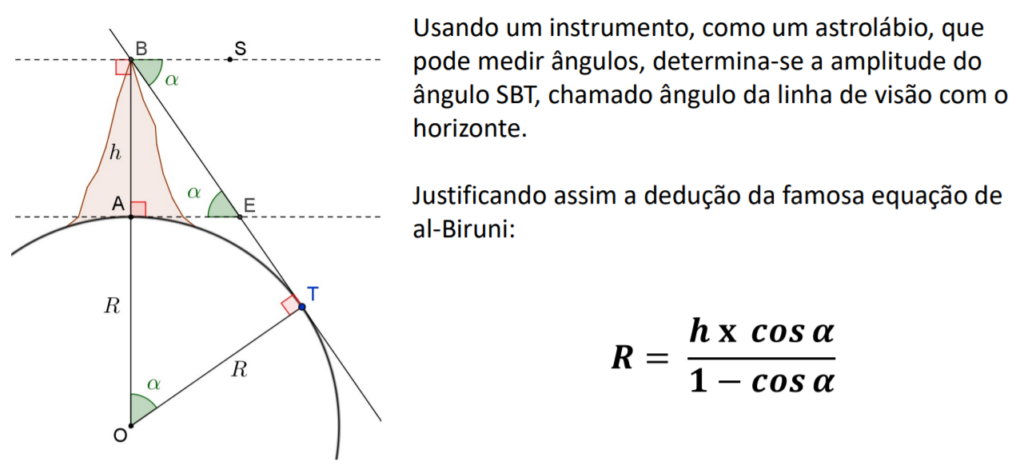
Os ângulos EBS e AEB são congruentes, pois são ângulos alternos internos.
Os triângulos retângulos [ABE] e [BOT] são semelhantes, pois o ângulo OBT é um ângulo interno comum.
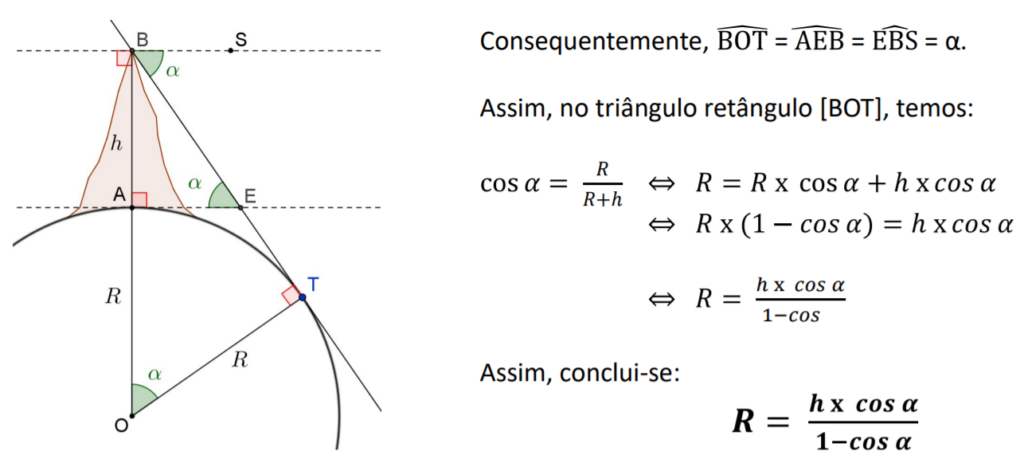
Digamos que estejamos em uma montanha a 2.000 metros. O ângulo de inclinação do horizonte é cerca de 1,43546 °. Conectando isso à fórmula:
2000 / (sec (1,43546 °) -1) = 6,371 × 10⁶
Fontes:
https://flatearthbusted.blogspot.com/2016/09/how-al-biruni-calculated-circumference.html
https://phobos.ramapo.edu/~ldant/honors/measure.pdf
https://www.acasinhadamatematica.pt/?p=12381
http://www.jphogendijk.nl/biruni.html
https://unesdoc.unesco.org/ark:/48223/pf0000074875
Publicação elaborada com a primorosa ajuda técnica do Eng. Carlos Lima
