Tanto para os programas de modelagem computacional, quanto para os cálculos manuais, a necessidade de simplificação se torna necessária para efeitos didáticos, de treinamento ou conceituação.
Conceitos fundamentais são isolados e algumas variáveis (variáveis estas que aumentam a já complexa matemática utilizada nos modelos) são ignoradas para que o resultado almejado forneça uma aproximação matemática. Obviamente tais variáveis afetam em maior ou menor grau quando a aplicação ocorre no mundo real, no entanto, as simplificações são úteis para desenvolver conceitos.
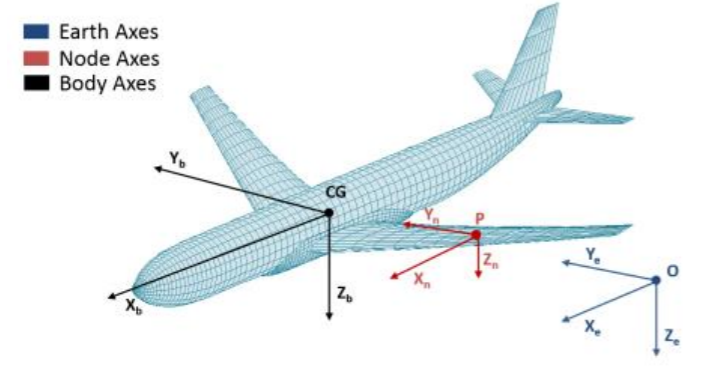
Para linearizar um modelo de voo não linear para fins de simplificação, é necessário assumir esses critérios, caso contrário, não seria mais LINEAR. Álgebra linear é usada para fazer aproximações de modelos não lineares. Se a massa mudar, os cálculos não serão mais lineares. Se o vetor de gravidade mudar através de uma terra esférica, não seria LINEAR.
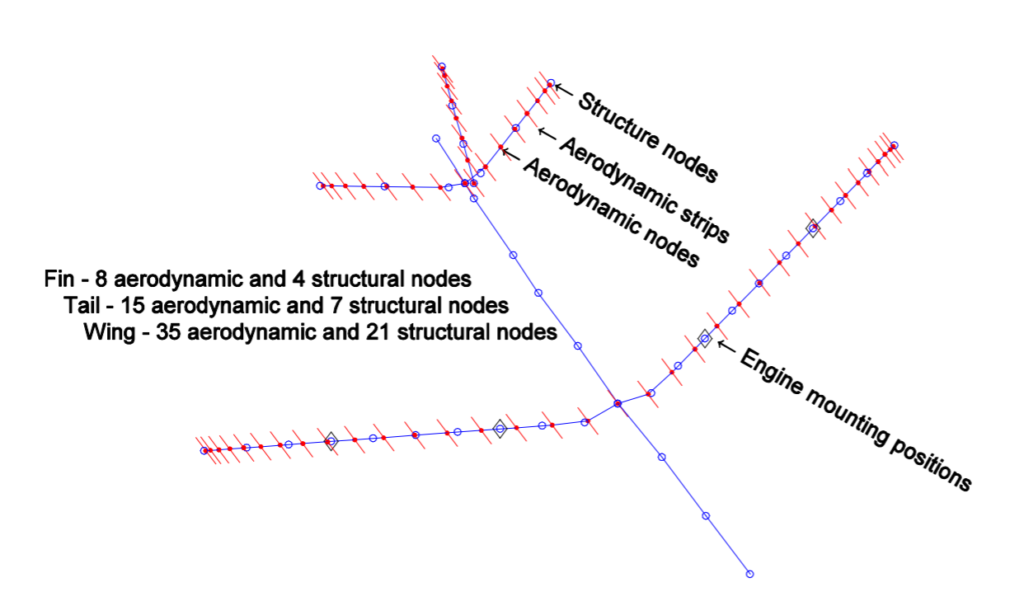
Um plano euclidiano com massa constante são demandas para linearizar a matemática. Os artigos em questão estão articulando o processo usado para linearizar um modelo para aproximações mais rápidas.
Se um voo ocorresse com aeronaves de massa constante em um plano no mundo real, o modelo linear seria o único existente, e também não haveria a necessidade de desenvolver documentos sobre o processo de linearização.
Numa época em que o poder computacional era limitado e caro, a simplificação para fins de estudos da dinâmica de manobras se fazia necessária, uma vez que estamos tratando de material da década de 80.
Conforme a complexidade da modelagem aumenta, os modelos podem incluir massas variáveis, como ocorre no artigo “Modeling and Simulation of Flight Dynamics of Variable Mass Systems” onde não ocorre a simplificação da massa constante que é utilizada nos artigos de modelagem linear.
No artigo “Tensor Flight Dynamics“, o Prof. Peter Zipfel listou os vários modelos de voo que criou. Ele usou o modelo plano para problemas mais simples, como aviões de combate e mísseis ar-a-ar. Para outros modelos como um míssil de cruzeiro, ele usou o modelo esférico. E para problemas mais complexos, como foguetes e mísseis de cruzeiro hipersônico, ele usou o modelo WGS84.
O raciocínio da simplificação utilizado nos artigos de modelagem linear é bastante simples, discutem a dinâmica de voo em manobras das aeronaves, tal qual o Prof. Zipfel fez para resolver os problemas mais simples.
A título de exemplo, uma bola lançada é afetada por muitos fatores, incluindo a resistência ao ar, a curvatura da Terra, a velocidade e a direção do vento, a rotação da Terra em torno do Sol, a órbita do Sol em torno da galáxia, a estrutura física da bola, sua massa, etc. Se quisermos calcular o caminho percorrido pela bola, muitas destas variáveis podem ser ignoradas, e os resultados serão praticamente corretos, uma vez que tais variáveis pouco ou nenhuma influencia exercem sobre o resultado.
Mas por que plano se a Terra é esférica?
RESPOSTA: Ao longo da curta distância que essas manobras ocorrem, a curvatura da Terra é insignificante, uma vez que na superfície da Terra temos apenas 1 grau de curvatura a cada 111 km aproximadamente. Mesmo em longas distâncias, o vetor de aceleração aponta em direção ao chão, o que matematicamente é o mesmo que manter sempre a altitude para acompanhar a curvatura da Terra, tal qual uma embarcação faz no mar.
Mas por que ignora a rotação da Terra?
RESPOSTA: Tanto a aeronave quanto a atmosfera estão solidários á Terra. Sob o referencial da Terra não há rotação, assim como dentro de um trem em movimento, um passageiro sentado está parado em relação a outros passageiros.
O referencial é importantes pois ajuda a remover variáveis desnecessárias.
Em todas as formas de análise, situações hipotéticas são aplicadas para simplificar os cálculos.
Teoricamente, a maneira mais precisa de calcular qualquer coisa seria modelando cada átomo com exatidão, cada movimento da Terra no sistema solar e cada movimento do sistema solar na galáxia, mas isso é proibitivamente demorado e requer um poder computacional dispendioso, no entanto, uma das principais habilidades da física é entender quais fatores precisam ser levados em consideração e o que podem ser ignorados para atingir o nível de precisão que se deseja dos resultados.
Fontes:
https://top-secret-documents.com/en/nasa/index.html
http://www.mezzacotta.net/100proofs/
https://www.metabunk.org/explained-nasa-documents-stating-a-flat-earth-linear-aircraft-models.t8992/
https://www.sciencedirect.com/topics/engineering/flight-dynamics

