Cálculo de rotas aéreas

Por William das Neves

1 – Distâncias ortodrômicas

A menor distância entre duas localidades no planeta Terra corresponde a um arco que liga as localidades. Esse arco é a distância ortodrômica.

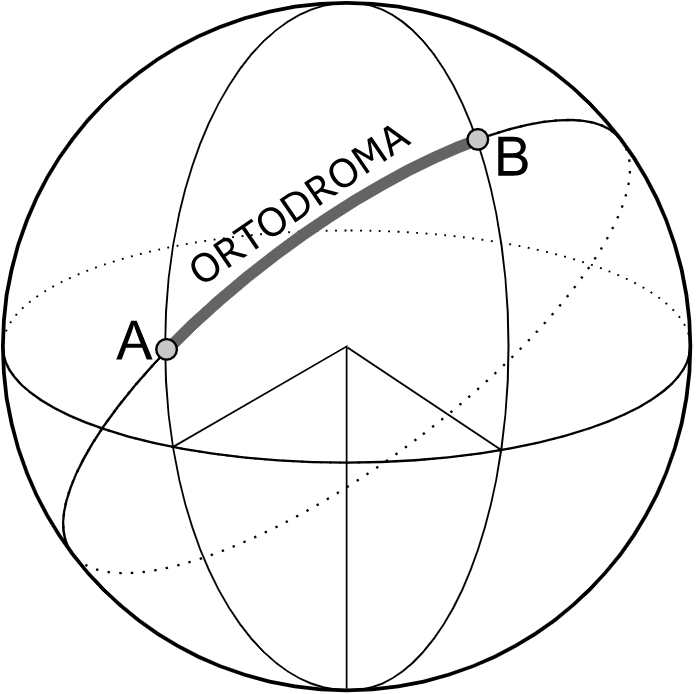
Figura 1: Exemplo de uma ortodrômica (arco A B)

Para calcular a distância entre duas localidades, usa-se a fórmula da ortodrômica, ou lei dos cossenos, originada num triângulo esférico. Veja a imagem do triângulo esférico ABC abaixo.

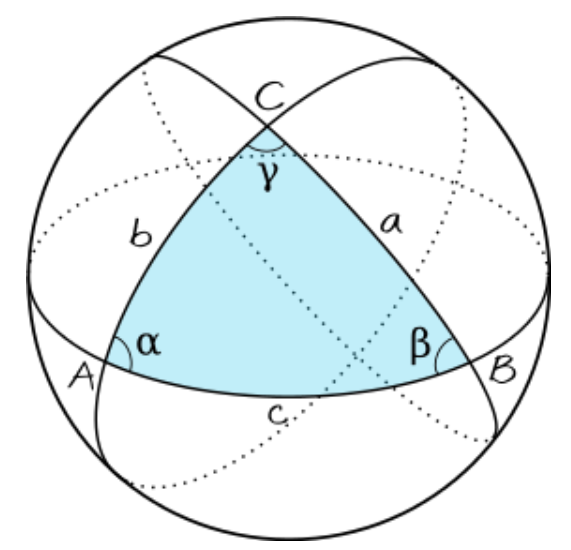
Figura 2: Exemplo de triângulo esférico ABC.

A fórmula da ortodrômica para calcular o comprimento do arco AB na figura 1 é: CosAB=senA.senB+cosA.cosB.cosDLO (1)
Onde:

A: latitude do local de partida
B: latitude do local de chegada
DLO: diferença de longitudes entre as localidades

No caso, essa diferença de longitudes é dada por:
DLO = longitude do local de chegada – longitude do local de partida

Importante ficar atento as convenções dos sinais adotados para as latitudes e longitudes das localidades. Assim são as convenções:

Latitude	Longitude
Norte (N): Positiva	Leste (L): Positiva
Sul (S): Negativa	Oeste (O): Negativa

Essa fórmula encontra o comprimento do arco AB medido em graus. Como a ortodrômica é a menor distância entre as localidades, o comprimento do arco AB é menor do que 180°, isto é, AB<180°.
Interessante usar outra expressão para auxiliar o cálculo da distância entre as duas localidades. Observando-se o arco mostrado na figura abaixo.

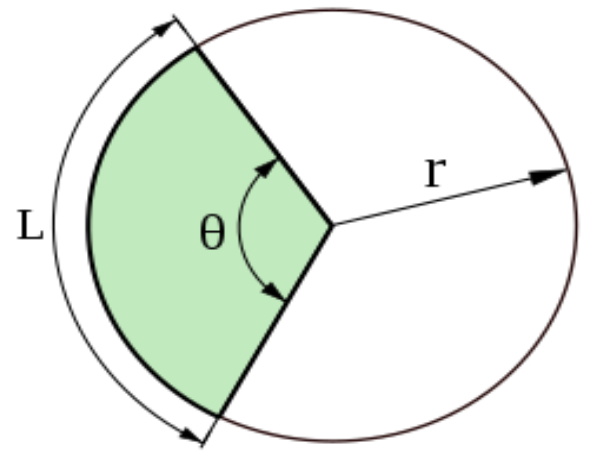
Vemos que o comprimento do arco L é dado por: L=r.⊙ (2)

Pode-se escrever a expressão (2), para calcular a distância entre as duas localidades no planeta terra da seguinte forma: D=R_T.AB. (3)

Onde:

R_T: raio da terra( pode-se adotar 6.371 km)
AB: comprimento do arco da ortodrômica medido em radianos.

Assim a distância ortodrômica será calculada usando as expressões (1) e (3).

Exemplos:

1 – Seja o voo GOL, GLO 2250, partindo do Rio de Janeiro (ICAO SBRJ), com coordenadas geográficas 22° 54′ 36″S e 43° 09′ 45″O a Porto Alegre (ICAO SBPA), com coordenadas geográficas 29° 59′ 38″ S e 51° 10′ 16″ O. Calcule a distância ortodrômica, em km, entre os aeroportos.

Resolução:

As coordenadas geográficas das localidades:

Local de partida SBRJ

22°54’36”S = – 22,91°
43°09’45”O = – 43,1625°

Local de Chegada SBPA

29°59’38″S = – 29,994°
51°10’16″O = – 51,1711°

Calculando a diferença de longitudes DLO.

DLO = longitude do local de chegada – longitude do local de partida
DLO = (-51,1711°) – (-43,1625°)
DLO = -8,0086°

Usando a fórmula da ortodrômica tem-se.

Cosd = senA.senB +cosA.cosB.cosDLO (1)

Onde

A: latitude do local de partida
B: latitude do local de chegada
DLO: diferença de longitudes
d: comprimento do arco medido em graus

Substituindo os dados na expressão (1) tem-se.

Cosd = sen(-22,91°).sen(-29,994°)+cos(-22,91°).cos(-29,994°).cos(-8,0086°)

Cosd = 0,9845860022

d = arccos(0,9845860022) = 10,0729043711°

Esse é o comprimento do arco que vai do aeroporto do Santos Dumont (SBRJ) até o aeroporto Salgado Filho (SBPA).

Transformando o comprimento do arco obtido em radianos tem-se.

3,14(pi)rad_________180°
d rad,______________10,0729043711°
d = (3,14 × 10,0729043711°)/180°
d = 0,1758053465 rad

Para calcular a distância entre os dois aeroportos, usa a expressão (3)

D = R_T.d

Onde

R_T: Raio da Terra igual a6.371 km
d: comprimento do arco medido em radianos

Logo a distância entre os dois aeroportos é de:

D = 6.371×0,1758053465 =1.120,1 km

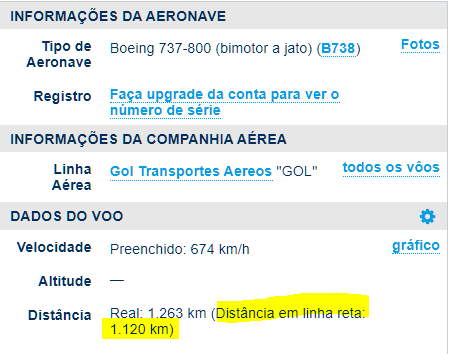
Verificando a distância do voo no site flightaware, a distância ortodrômica entre os aeroportos indicada é cerca de 1.120 km.

https://pt.flightaware.com/live/flight/GLO2250

*A distância real é aquela efetivamente percorrida pela aeronave,* no planejamento de voo há procedimentos de saída, chegada e aproximação previstos em cartas aéreas que devem ser cumpridos pela tripulação em comando, além de fatores como condições meteorológicas no momento e etc.

2 – Seja a carta de saída padrão por instrumentos do aeroporto de Natal RNAV IBAGA 1C-OGPER 1C-RATEP 1B-RUMBA 1A-SAFUC 1V-SEVIL 1A RWY 34R

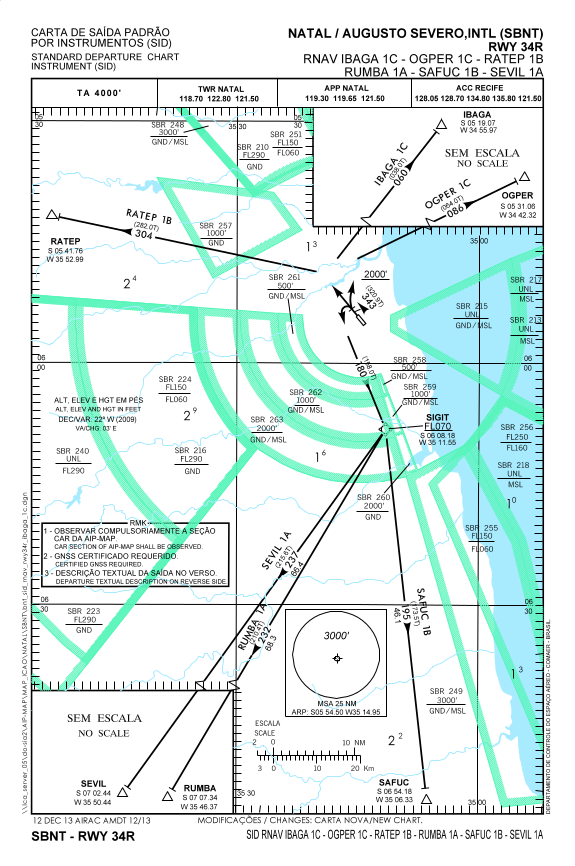
http://ais.decea.gov.br/download/?arquivo=48c1c5dc-897a-1031-95e7-72567f175e3a&apikey=1587263166.

Calcule a distância ortodrômica do waypoint SIGIT, com coordenadas geográficas S6°8,18’ e W35°11,55,’ ao waypoint SEVIL, com coordenadas geográficas S7°2,44’ e W35°50,44’, em milhas náuticas.

Resolução:

As coordenadas geográficas das localidades.

SIGIT
S6°08,18’=-6,1363°
W35°11,55’=-35,1925°

SEVIL
S7°2,44’=-7,0407°
W35° 50,44’= -35,8407°

A diferença de longitudes

DLO = longitude do local de chegada – longitude do local de partida
DLO=Chegada-partida
DLO=(-35,8407°)-(-35,1925°)
DLO= -0,6482°

Usando a fórmula da ortodrômica tem-se.

Cosd = senA.senB +cosA.cosB.cosDLO (1)

Onde

A: latitude do local de partida
B: latitude do local de chegada
DLO: diferença de longitudes
d: comprimento do arco medido em graus

Substituindo os dados na expressão (1) tem-se.

cosd=sen(-6,1363°).sen(-7,0407°)+cos(-6,1363°).cos(-7,0407°).cos(-0,6482°)

cosd=0,9998122759
d=arccos(0,9998112259)
d=1,1102082234°

Esse é o comprimento do arco que vai do waypoint SIGIT até SEVIL.

Transformando o valor obtido em radianos.

3,14(pi) rad______180°
d rad____________1,1102082234°
d=0,0193767889 rad

A distância ortodrômica entre os waypoints SIGIT e SEVIL, em km, é:

D=R_T.d (Com raio da terra=6.371km)
D=6.371km × 0,0193767889
D=123,45 km

Transformando a distância D obtida em milhas náuticas (NM).

1NM_______1,852 KM
D__________123,45 KM
D=123,45/1,852=66,7NM

De acordo com a carta aeronáutica, a distância entre os waypoints é de 66,4 milhas náuticas.

2 – Azimute esférico

O azimute é o ângulo formado no sentido horário entre o norte e uma direção determinada. Esse ângulo varia entre 0° a 360°. Veja a figura abaixo:

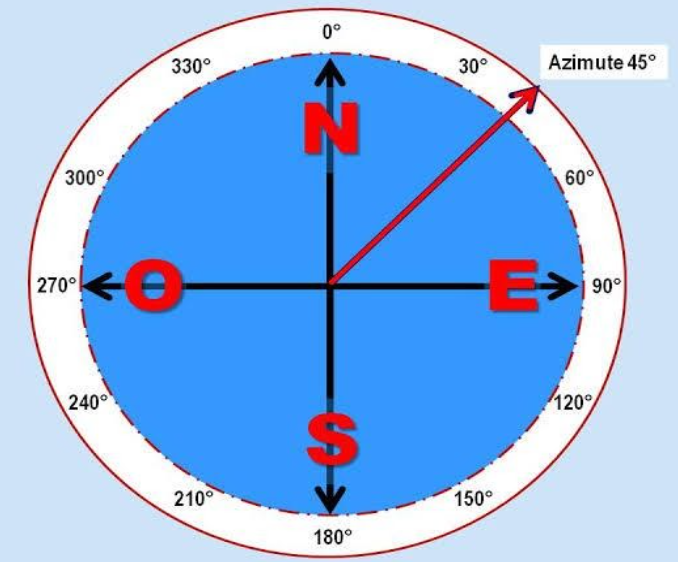
Para calcular o azimute esférico, usa a seguinte expressão:

A_z= arctg(senDLO/cosA.tgB – senA.cosDLO) (1)

Onde:

DLO: diferença de longitudes entre os pontos
A: latitude do ponto de partida
B: latitude do ponto de chegada

Para o cálculo de azimute esférico, também é importante observar as convenções dos sinais adotados para as latitudes e longitudes das localidades.

Latitude	Longitude
Norte (N): Positiva	Leste (L): Positiva
Sul (S): Negativa	Oeste (O): Negativa

Exemplos

Abaixo serão calculados os azimutes esféricos em cartas aeronáuticas

1 – Seja a carta de saída padrão por instrumentos do aeroporto de Natal RNAV IBAGA 1C-OGPER 1C-RATEP 1B-RUMBA 1A-SAFUC 1V-SEVIL 1A RWY 34R Disponível no site do DECEA

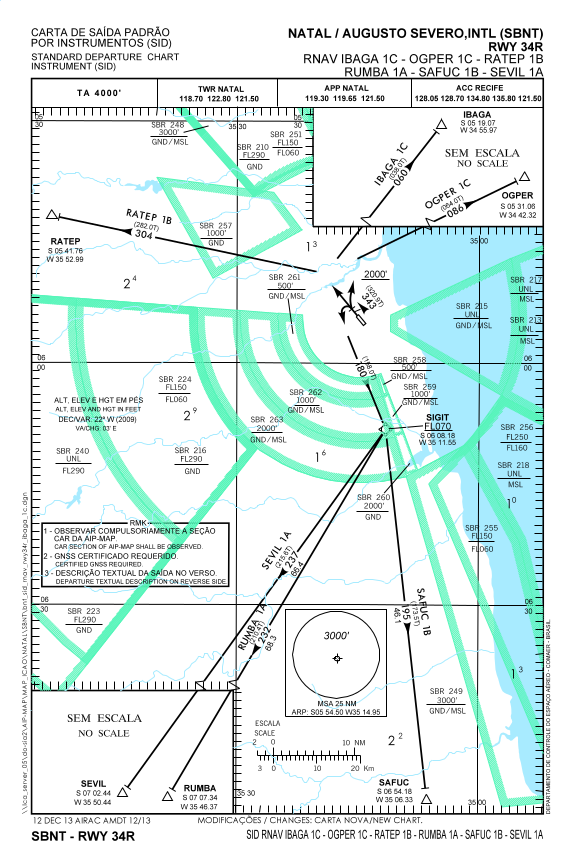
Calcule o azimute que vai do waypoint SIGIT, cujas coordenadas geográficas são S 6°08,18′ e W35° 11,55′, ao waypoint SEVIL, cujas coordenadas geográficas são S 7°2,44′ e W35° 50,44′.

Resolução:

Coordenadas geográficas

SIGIT

S 6°08,18’= -6,1363°
W35° 11,55’= -35,1925°

SEVIL

S 7°2,44’= -7,0407°
W35° 50,44’= -35,8407°

O azimute esférico é dado pela expressão (1)

A_z=arctg(senDLO/cosA.tgB – senA.cosDLO) (1)

Onde:

A: latitude do ponto de partida
B: latitude do ponto de chegada
DLO: diferença de longitudes

A diferença de longitudes (DLO)

DLO= Chegada – partida
DLO= (-35,8407°) – (-35,1925°)
DLO= -0,6482°

Assim substituindo os dados na equação (1):

A_z=arctg(sen(-0,6482°)/cos(-6,1363°).tg(-7,0407°)-sen(-6,1363°).cos(-0,6482°))

A_z=arctg(−0,0113129829/ −0,0159108699)

A_z =arctg(0,711022274)

O valor acima, 0,711022274, está no 1° ou 3° quadrante porque a tangente é positiva nesses quadrantes.

Para o primeiro quadrante temos:

A_z=arctg(0,711022274)= 35,4136746095°

Para o terceiro quadrante temos:

A_z= arctg(0,711022274)= 215,4136746095°

Uma forma de definir em qual quadrante está o azimute é analisar a variação dos sinais das funções seno, cosseno e tangente nos 1°, 2°, 3° e 4° quadrante conforme a tabela abaixo.

Função	1°quadrante	2°quadrante	3°quadrante	4°quadrante
Seno	Positiva	Positiva	Negativa	Negativa
Cosseno	Positiva	Negativa	Negativa	Positiva
Tangente	Positiva	Negativa	Positiva	Negativa

A função tangente é definida como:

tgx = seno/cosseno

O valor arctg (−0,0113129829/ −0,0159108699) tem um sinal negativo no numerador (seno) e negativo no denominador (cosseno). Assim consultando a tabela com a variação dos sinais das funções. O 3° quadrante apresenta o seno e cosseno com sinais negativos e a função tangente positiva. Logo o azimute se encontra no 3°quadrante.

No caso 3° quadrante. Logo:

A_z=215,4°

2 – Dada a carta de chegada padrão por instrumentos do aeroporto de Recife RNAV CPG B-ILNOT BSAFUC B-SEVIL B RWY 36 disponível no site do DECEA

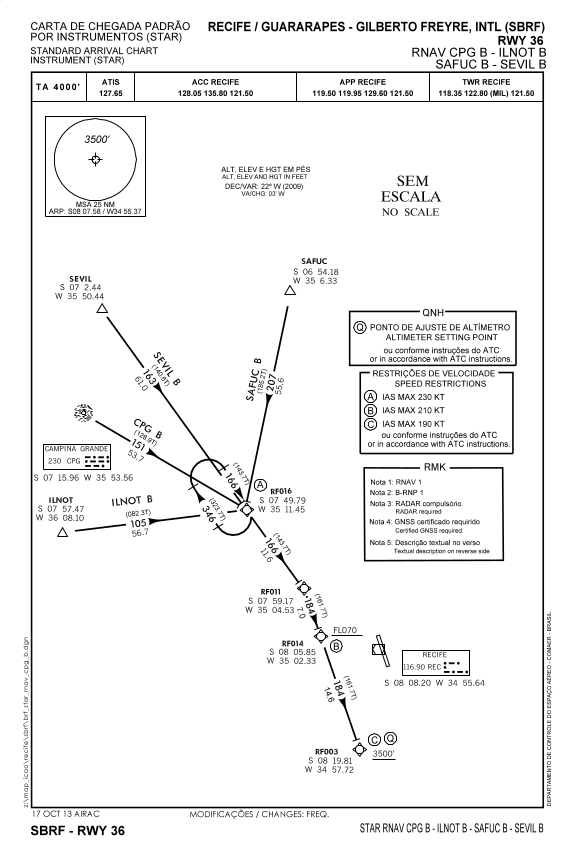
Determine:

a) O azimute que vai do waypoint SEVIL, cujas coordenadas geográficas são S7°2,44’ e W35°50,44’, ao waypoint RF016, cujas coordenadas geográficas são S7°49,79’ e W35°11,45’.

Resolução

Coordenadas geográficas

SEVIL

S7°2,44’ = -7,0407°
W35°50,44’ = -35,8407°

RF016

S7°49,79’ = -7,8298°
W35°11,45’= -35,1908°

O azimute esférico é dado pela expressão (1)

Az=arctg(senDLO/cosA.tgB – senA.cosDLO) (1)

Onde:

A: latitude do ponto de partida
B: latitude do ponto de chegada
DLO: diferença de longitudes

A diferença de longitudes (DLO)

DLO= Chegada – partida
DLO = (-35,1908°) – (-35,8407°)
DLO = 0,6499°

Assim substituindo os dados na equação (1):

A_z=arctg(sen(0,6499°)/cos(-7,0407°).tg(-7,8298°)–sen(-7,0407°).cos(0,6499)

A_z=arctg(0,0113426516/−0,0139094455)

A_z = arctg(−0,8154639666)

O valor acima ,– 0,8154639666, está no segundo ou quarto quadrante pois a tangente é negativa nesses quadrantes.

Para o segundo quadrante temos:

A_z=arctg(-0,8154639666) = 140,8039961446°

Para o quarto quadrante temos:

A_z=arctg(-0,8154639666) =320,8039961446°

Uma forma de definir em qual quadrante está o azimute é analisar a variação dos sinais das funções seno, cosseno e tangente nos 1°, 2°, 3° e 4° quadrante conforme a tabela abaixo.

Função	1°quadrante	2°quadrante	3°quadrante	4°quadrante
Seno	Positiva	Positiva	Negativa	Negativa
Cosseno	Positiva	Negativa	Negativa	Positiva
Tangente	Positiva	Negativa	Positiva	Negativa

A função tangente é definida como:

tgx = seno/cosseno

O valor arctg(0,0113426516/−0,0139094455) tem sinal positivo no numerador (seno) e negativo no denominador(cosseno). Verificando na tabela acima, isso ocorre quando o seno e o cosseno estão no 2°quadrante e a tangente é negativa.

Logo o azimute está no 2° quadrante:

A_z =arctg(-0,8154639666) = 140,8039961446°

b) O azimute que vai do waypoint ILNOT, cujas cordenadas geográficas são S7°57,47’ e W36°8,10’ ao waypoint RF016, cujas coordenadas geográficas são S7°49,79’ e W35°11,45’.

Resolução:

Coordenadas geográficas.

ILNOT

S7°57,47’= -7,958°
W36°8,10’= -36,135°

RF016

S7°49,79’= -7,8298°
W35°11,45’= -35,1908°

O azimute esférico é dado pela expressão (1)

Az=arctg(senDLO/cosA.tgB – senA.cosDLO) (1)

Onde:

A: latitude do ponto de partida
B: latitude do ponto de chegada
DLO: diferença de longitudes

A diferença de longitudes (DLO)

DLO= Chegada – partida
DLO= (-35,1908°) – (-36,135°)
DLO= 0,9442°

Assim substituindo os dados na equação (1):

A_z=arctg(sen(0,9442°)/cos(-7,958°).tg(-7,8298°) – sen(-7,958°).cos(0,9442°)

A_z=arctg(0,0164786529/0,0022397679)

A_z=arctg(7,3573038081)

O valor acima, 7,3573038081, é positivo. A tangente é positiva no 1° e 3° quadrante. Assim o azimute pode ser:

Para o 1° quadrante:

A_z=arctg(7,3573038081)= 82,2598261189°

Para o 3° quadrante:

A_z=arctg(7,3573038081)= 262,2598261189°

Uma forma de definir em qual quadrante está o azimute é analisar a variação dos sinais das funções seno, cosseno e tangente nos 1°, 2°, 3° e 4° quadrante conforme a tabela abaixo.

Função	1°quadrante	2°quadrante	3°quadrante	4°quadrante
Seno	Positiva	Positiva	Negativa	Negativa
Cosseno	Positiva	Negativa	Negativa	Positiva
Tangente	Positiva	Negativa	Positiva	Negativa

A função tangente é definida como:

tgx= seno/cosseno

O quociente arctg(0,0164786529/0,0022397679) tem um valor positivo no numerador(seno) e positivo no denominador (cosseno). Assim consultando a tabela para saber onde o seno e cosseno são positivos, o quadrante é o 1°.

Logo o azimute será:

A_z=arctg(7,3573038081)= 82,2598261189°

3 – Latitudes e Longitudes

Latitude é o ângulo formado entre o equador e a normal à superfície do planeta. A latitude define a distância, medida em graus, ou posição do ponto na superfície do planeta em relação a linha do equador. Esse ângulo que representa a latitude varia entre 0 a 90° no hemisfério norte e 0 a -90° no hemisfério sul como na figura abaixo.

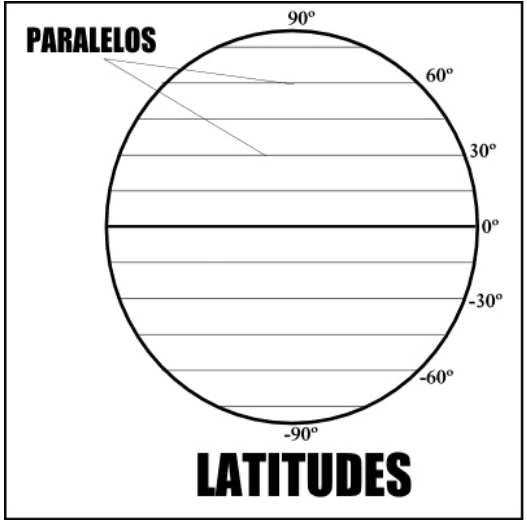
A longitude tem como referência o meridiano de Greenwich. O ângulo diedro formado entre o meridiano astronômico e o meridiano de Greenwich é a longitude. Esse ângulo varia entre 0 a 180° à leste e 0 a -180° à oeste. Pode-se dizer que a longitude informa a distância ou posição do ponto em relação ao meridiano de Greenwich. Veja a longitude na figura abaixo.

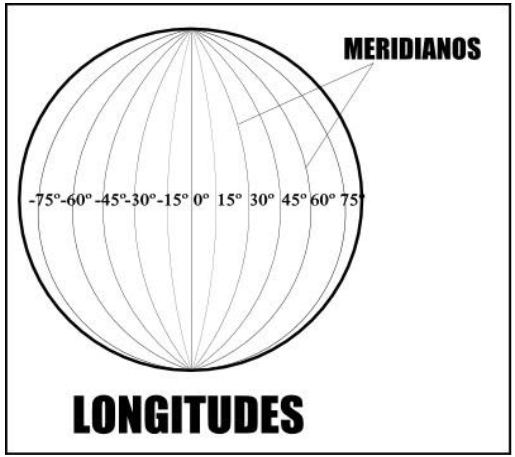
Agora vamos pensar na seguinte situação: Partindo de um ponto de coordenadas geográficas conhecidas, seguindo um azimute conhecido e percorrendo uma distância determinada, como encontrar as coordenadas geográficas do local de chegada?

Para responder essa questão, recorremos a navegação em triângulos esféricos. Dessa forma, pode-se encontrar as coordenadas geográficas do local de chegada.

Para encontrar a latitude do local de chegada, tem a expressão matemática abaixo:

senLa = senA.cosd + cosA.send.cosA_z.(1)

Onde:

La: latitude do local de chegada (Positiva no hemisfério Norte e negativa no hemisfério Sul)
A: latitude do local de partida;
A_z: azimute que vai de um local ao outro;
d = distância percorrida em milhas náuticas entre os pontos / 60

A determinação da longitude do local de chegada é obtida por meio das seguintes expressões (2) e (3).

Lo_f = Lo_i + DLO (2)

DLO = arctg(senA_z/cosA.cotgd – senA.cosA_z) (3)

Onde:

A_z : azimute;
A: latitude do ponto de partida;
d = distância percorrida em milhas náuticas entre os pontos / 60

Exemplos

Serão utilizadas cartas aeronáuticas disponibilizadas no site do DECEA.

1 – Seja a carta de saída padrão por instrumentos do aeroporto de Natal RNAV IBAGA 1C-OGPER 1C-RATEP 1B-RUMBA 1A-SAFUC 1V-SEVIL 1A RWY 34R disponível no site do DECEA

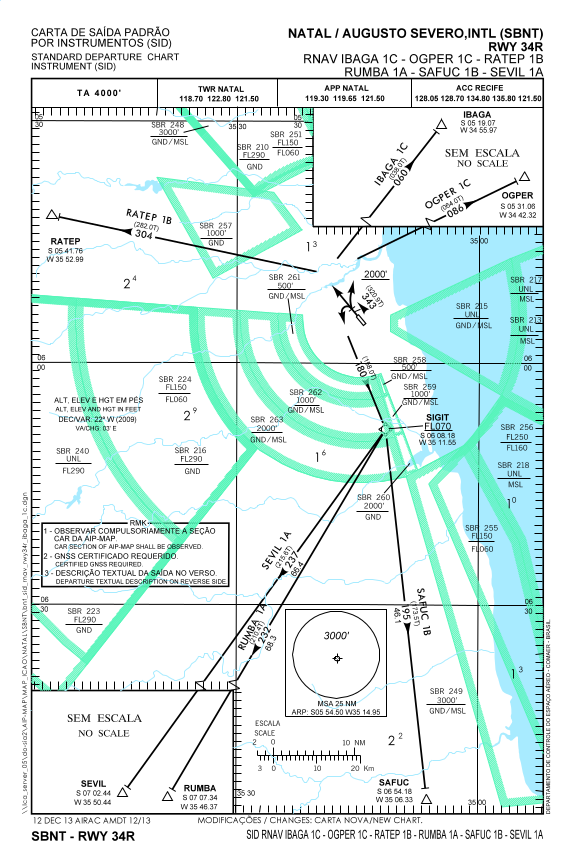
Sabendo que na execução desse procedimento ao passar pelo waypoint SIGIT, cujas coordenadas geográficas são S6°8,18’ e W35°11,55’, o avião seguirá no azimute 210,4° (aqui não considera o azimute magnético) percorrerá uma distância de 68,3 milhas náuticas até chegar no waypoint RUMBA. Quais as coordenadas geográficas do waypoint RUMBA?

Resolução

As coordenadas geográficas

SIGIT

S6°8,18’= -6,1363°
W35°11,55’= -35,1925°

Azimute que vai de SIGIT até RUMBA

A_z=210,4°

O valor de “d”.

d= distância percorrida em milhas náuticas entre os pontos / 60
d= 68,3 / 60 = 1,1383°

Determinando a latitude usando a expressão (1):

senLa = senA.cosd + cosA.send.cosA_z_.

senLa = sen(-6,1363°).cos(1,1383) + cos(-6,1363°).sen(1,1383°).cos210,4°
senLa = -0,1239095392
La = arcsen(-0,1239095392)
La= -7,1177874153° (4°quadrante)

O valor encontrado para latitude com sinal negativo indica que ponto está no hemisfério Sul. Assim a latitude será:

La= S7°7,1’ (faça 0,1177874153 x 60 para encontrar os minutos)

Para encontrar a longitude, usa inicialmente a expressão (3) para determinar a diferença de longitudes DLO entre os waypoints.

DLO = arctg(senA_z/cosA.cotgd – senA.cosA_z)
DLO= arctg(sen210,4°/cos(-6,1363°).cotg(1,1383°) – sen(-6,1363°).cos210,4°)
DLO= arctg(-0,010131346)= -0,5804635067°

Uma vez que se sabe a diferença de longitudes, agora usa a expressão (2) para encontrar a longitude do waypoint RUMBA.

Lo_f = Lo_i + DLO

Lo_f= (-35,1925°) + (-0,5804635067°)
Lo_f = – 35,7729635067°

O valor negativo indica o waypoint está localizado no oeste. Assim a longitude será:

Lo_f= W35°46,37’ (faça 0,7729635067 x 60 para encontrar os minutos)

Portanto as coordenadas geográficas do waypoint RUMBA são:

S7°7,1’ e W35°46,37’

2 – Seja a carta de chegada padrão por instrumentos do aeroporto de Recife RNAV CPG B-ILNOT BSAFUC B-SEVIL B RWY 36 disponível no site do DECEA

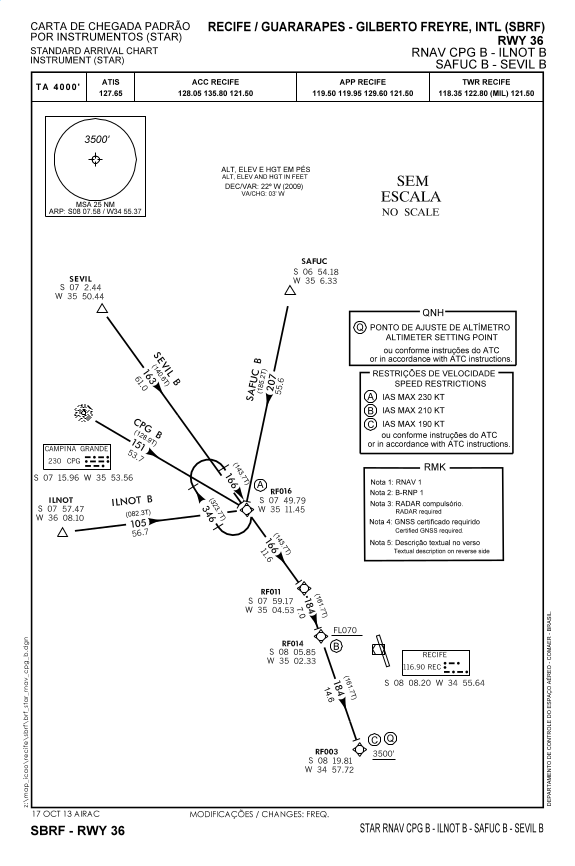
O avião inicia o procedimento a partir do waypoint ILNOT, cujas coordenadas geográficas são S7°57,47’ e W36°8,10, percorre uma distância de 56,7 milhas náuticas, seguindo no azimute 82,3° (não é o azimute magnético) e chega até o waypoint RF016. Quais as coordenadas geográficas do waypoint RF016?

Resolução:

As coordenadas geográficas:

S7°57,47’= -7,958°
W36°8,10’= -36,135°

O azimute que vai de ILNOT até RF016

A_z=82,3°

O valor de “d”.

d= distância percorrida em milhas náuticas entre os pontos / 60
d= 56,7 / 60 = 0,945°

Determinando a latitude usando a expressão (1):

senLa = senA.cosd + cosA.send.cosA_z.

senLa = sen(-7,958°).cos(0,945°) + cos(-7,958°).sen(0,945°).cos82,3°

senLa= -0,1362398269
La= arcsen(-0,1362398269)
La= -7,8303191762°

O sinal de menos indica que o waypoint está localizado no hemisfério Sul. Assim:

La= S7°49,8’ (faça 0,8303191762 x 60 para obter os minutos)

Para encontrar a longitude, usa inicialmente a expressão (3) para determinar a diferença de longitudes DLO entre os waypoints.

DLO = arctg(senA_z/cosA.cotgd – senA.cosA_z)

DLO = arctg(sen82,3°/cos(-7,958°).cotg(0,945°) – sen(-7,958°).cos82,3°)
DLO= arctg(0,0164999754)
DLO= 0,9452931736°

Uma vez que se sabe a diferença de longitudes, agora usa a expressão (2) para encontrar a longitude do waypoint RF016.

Lo_f = Lo_i + DLO

Lo_f= (-36,135°) + (0,9452931736°)
Lo_f= -35,1897068264° (faça 0,1897068264 x 60 para encontrar os minutos)

O sinal de menos indica que o waypoint está localizado no oeste. Assim a longitude será:

Lo_f=W35°11,4’

Portanto as coordenadas geográficas do waypoint RF016

S7°49,8’ e W35°11,4’

Fontes:

http://www.cartografica.ufpr.br/portal/wp-content/uploads/2011/10/aula08a-Terra-Esférica-ortodromica.pdf

http://www.cartografica.ufpr.br/docs/Nadal/APLICA%C3%87%C3%95ES%20DA%20TRIGONOMETRIA%20ESF%C3%89RICA%20NA%20CARTOGRAFIA%20E%20NA%20ASTRONOMIA.pdf