Introdução
Durante observações em campo, nos famosos “testes de curvatura”, a compreensão dos efeitos da refração por parte do público leigo normalmente é bastante caótica.
Nesta publicação será efetuada uma análise sistemática de todas as variáveis que possuem influência sobre o índice de refração do ar atmosférico, assim como a construção de um gradiente de refração, esclarecendo seu comportamento e quais as condições necessárias para a existência do aumento, diminuição, estabilização e inversão da refração
1 Índice de refração do ar padrão:
O índice de refração do ar padrão é obtido com ar seco na temperatura de 15°C submetido a uma pressão de 760 mm/Hg, e possui um valor n= 1,00030 comparado ao valor n=1 do vácuo, sendo utilizado como referência desde o início do século XX, por laboratórios de óptica em inúmeras aplicações.
A referência é necessária para os ajustes e correções da condição do ar, principalmente durante as medições com refratômetros laser ou outros equipamentos ópticos de precisão.
1.1 Variação do índice em função da pressão:
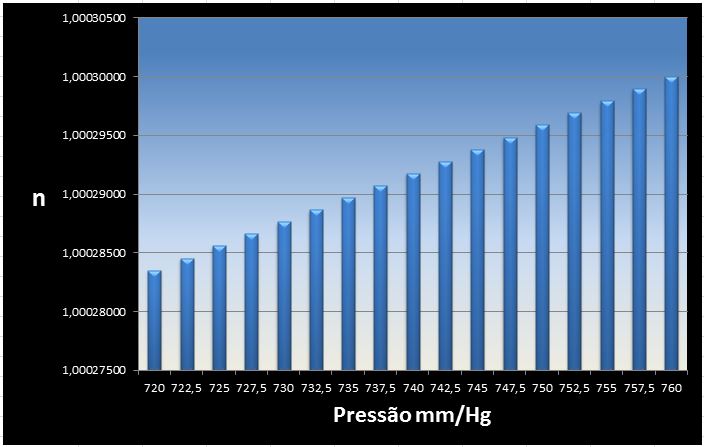
dn/dP|ar ≈ 3×10−7 mmHg−1 (sem correção de distribuição*)
Em condições normais, a cada 12 metros de elevação temos o declínio de -1 mm/Hg ou -0,0833 mm/Hg a cada metro. A diminuição da pressão diminui o índice de refração do ar.
1.1.1 Dependência com a concentração de CO2 e correção de distribuição*
O CO2, cuja concentração normal (0,03% por unidade de volume) contribui com uma pressão parcial de 0.23 Torr (1 mm/Hg = 1,00000023686 Torr) , de modo que a contribuição na refratividade padrão é de 4,175×10-8. A correção de distribuição deve ser feita com 9,31 x 10-9 / m sendo o valor final de 4,12 x 10-7 a cada mm/Hg:
- 0,23 Torr = 0,22999994552 mm/Hg
- Correção por distribuição: 0,223 mm/Hg x 4,175 x 10-8 = 9,31 x 10-9
- Valor normal: -0,0833 mm/Hg (1 metro) x 3 x 10-7 = 24,99 x 10-9
- Valor corrigido: (24,99 x 10-9 )+( 9,31 x 10-9 )= 34,3 x 10-9
- 34,3 x 10-9 / 0,0833 = 4,117 x 10-7
Portanto o valor final é de dn/dP|ar ≈ 4,12 × 10−7 mmHg−1
.
1.2 Variação do índice em função da temperatura:
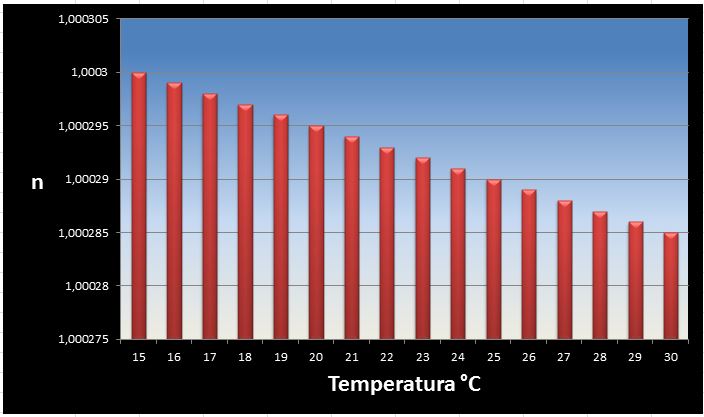
dn/dT|ar ≈ −1×10−6 °C−1
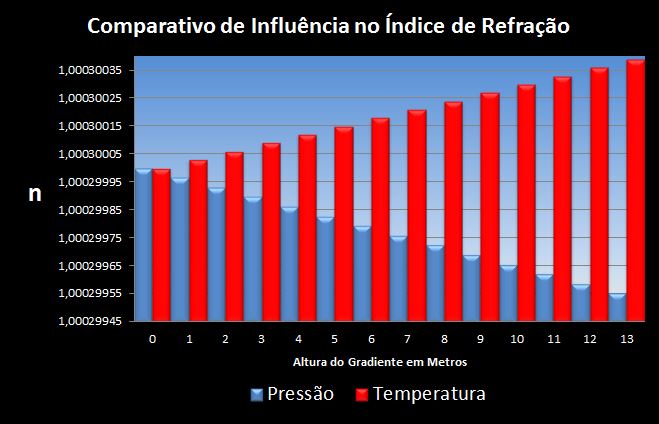
Nota-se que o aumento da temperatura gera uma redução no índice de refração. Em um primeiro momento podemos pensar que a variação de temperatura certamente supera com facilidade a mudança do índice ocasionada pela pressão. Isso é um raciocínio válido em amostras controladas, porém veremos que a distribuição desta variação em um gradiente atmosférico se comporta de outra forma, sendo necessário um resfriamento superior a -0,0315°C/m e condições propícias de umidade, temperatura, altura do gradiente e ponto de saturação (URmax) para o início da inversão em alguns casos.
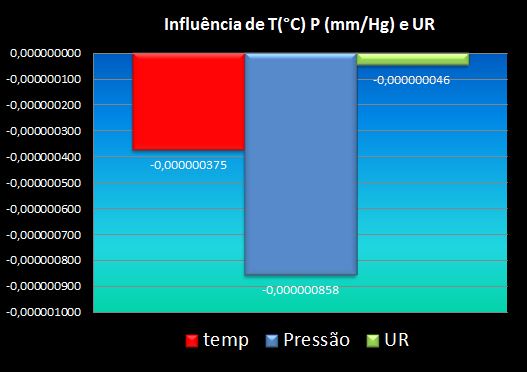
Abaixo três comparativos entre pressão e temperatura:
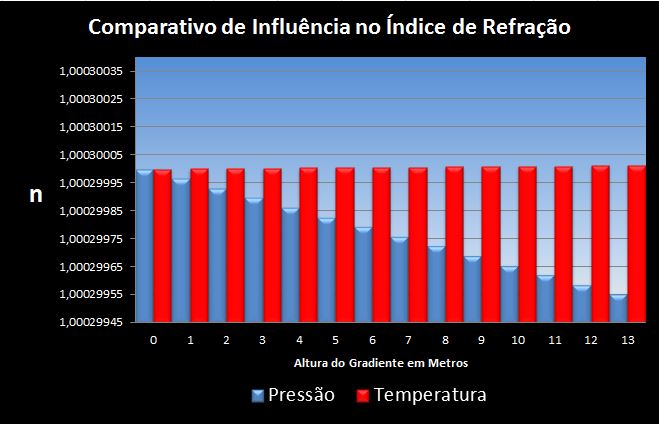
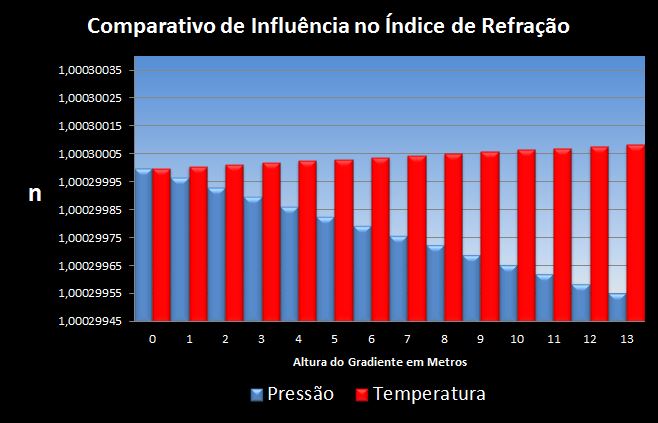
1.3 Variação do índice em função da umidade relativa (UR):
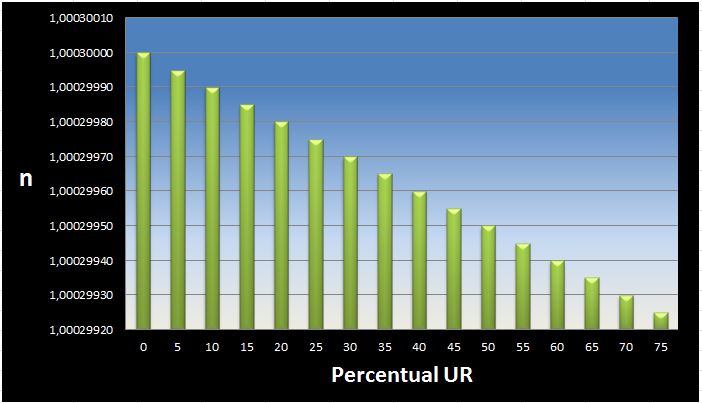
dn/d(UR)|ar ≈ −1×10−8 %−1
O aumento do percentual UR, diminui o índice de refração.
O cálculo necessário para a influência da variação percentual UR no gradiente (variação entre URinicial e URfinal ) envolve a obtenção do valor da umidade absoluta (massa do vapor de água em suspensão) para a temperatura inicial do gradiente e respectivo valor URinicial.
A correção para o índice inicial do gradiente é feita diretamente pelo valor de UR, com a devida atenção:
O referido valor inicial de -1 x 10-8 se aplica à variação da amostra com temperatura de 15°C e 760 mm/Hg. Com o aumento da temperatura e consequentemente o aumento da capacidade de absorção (Umidade Absoluta) de 2% (25°C) é necessária a correção numa ordem de -2,285 x 10-8 a cada grau acima da temperatura de referência (15°C).
2 Diferença da densidade do ar seco e ar úmido:
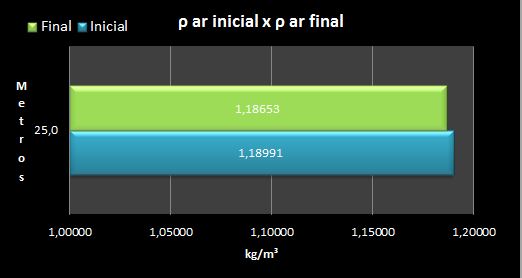
É muito importante obter os valores da densidade do ar com a correção por %UR e não somente por temperatura e pressão. Isso traduz valores mais precisos, já que o ar úmido é menos denso do que o ar seco. No cálculo de construção do gradiente, temos de verificar a densidade inicial e final do ar com a devida variação de percentual UR.
2.1 Cálculo para densidade do ar e massa de vapor água em suspensão:
Densidade do ar seco: kg/m3 (PressãoPa ×0,029)/((T°C+273,15)×8,314)
Umidade absoluta URmax e relativa (g/m3 ):((%UR÷100)×1330×e^((17,62×T°C)/(T°C+243,12))/((T°C+273,16))
2.1.1 Referência para a substituição de mols de H2O :
Massa molar H2O = 18,015 g/mol (1g de H2O = 0,0555 mols)
Mols de H2O = (H2O g/m3) x 0,0555 mols de H2O
Massa molar Ar Atmosférico = (78% N2, 21% O2, 1% (outros gases)) = 29 g/mol (1g de Aratm = 0,03448 mols)
Gramas de Aratm = (mols de H2O) / 0,03448 mols de Aratm
Exemplo 1- Diferença de densidade entre ar seco e saturado: 20°C 101325 Pa (100%UR) :
ρ Ar 20°C 101325 Pa (seco) = 1,2056 kg/m3
Gramas de H2O /m3 em URmax : (100÷100)×1330×e^((17,62×20)/(20+243,12))/((20+273,16))= 17,314 g/m3 (1,43% da massa total)
17,314 g/m3 x 0,0555 mols = 0,9609 mols H2O
Gramas de Aratm = 0,9609 / 0,03448 = 27,868 g de Aratm
27,868 g de Aratm – 17,314 g de H2O = 10,554 g/m3 (0,010554 kg/m3)
ρ Ar 20°C 101.325Pa (100% UR)= 1,2056 kg/m3 – 0,010554 kg/m3 = 1,1950 Kg/m3
ρ Ar seco: 1,2056 kg/m3
ρ Ar saturado: 1,1950 k/m3
Exemplo 2- Diferença entre ar seco e úmido: 20°C 101325 Pa (70% UR):
ρ Ar 20°C 101325 Pa (seco) = 1,2056 kg/m3
Gramas de H2O /m3 em UR70%:(70÷100)×1330×e^((17,62×20)/(20+243,12))/((20+273,16))= 12,119 g/m3 (1,0052 % da massa total)
12,119 g/m3 x 0,0555 mols = 0,67265 mols de H2O
Gramas de Aratm = 0,67265 / 0,03448 = 19,508 g de Aratm
19,508 g de Aratm – 12,119 g de H2O = 7,389 g/m3 (0,007389 kg/m3)
ρ Ar 20°C 101.325Pa (70% UR)= 1,2056 kg/m3 – 0,007389 kg/m3 = 1,1982 Kg/m3
ρ Ar seco: 1,2056 kg/m3
ρ Ar 70% UR : 1,1982 Kg/m3
2.2 Equação simplificada de substituição de mols para o cálculo de diferença de densidade ar seco e ar úmido/saturado:
Exemplo para Ar 20°C 101325 Pa saturado (100%UR) :
*Mvs = massa do vapor em suspensão (kg/m3 )
ρar úmido = ρar seco – (Mvs x 0,6096)
ρar úmido = 1,2056 kg/m3 – (0,017314 kg/m3 x 0,6096)
ρar úmido = 1,1950 kg/m3
3 Parâmetros de refração
A refração pode ser expressa por vários parâmetros que dependem uns dos outros:
Pressão inicial
dT/dH °C/m
Coeficiente de refração k → Coef. k
Refração-Fator a → Fator a
3.1 Coeficiente de refração k
O coeficiente de refração k é utilizado para a correção das posições observadas e as reais posições geométricas dos alvos, sendo imprescindível o seu uso em topografia, levantamentos geodésicos, astronomia de posição, entre outros. O coeficiente K , assim como o Fator “a”, não deve ser confundido com o valor do índice de refração!
O coeficiente de refração k é a razão entre o raio da terra “R” e o raio do arco do desvio da luz “RR” ou seja, é o resultado final ocasionado pela variação do índice de refração entre as camadas do gradiente. Se o gradiente tiver variações mais intensas, isso afeta diretamente o desvio luminoso:
k =(503(P/(T°C+273,15)^2))(0,0343+dT/dH)
RR = R/k
k= R/RR
R’ = R/(1-k)
Fator a =R’/R
Onde:
k =Coeficiente de Refração
R = Raio da Terra
R’= Raio geométrico observado
RR = Raio do desvio luminoso
P =Pressão do ar no observador em mbar ou hPa ou 1/100 Pa, Padrão = 1013,25 mbar (760 mm/Hg)
T =Temperatura no observador em Kelvin, Padrão = 288,15 K = 15 ° C
dT/dH = ° C / m, Padrão = −0,0065 ° C / m

Normalmente o resultado do coeficiente K ignora a variação ocasionada por diferença de UR, porém nos exemplos a seguir, isso também é calculado aprimorando o resultado final obtido.
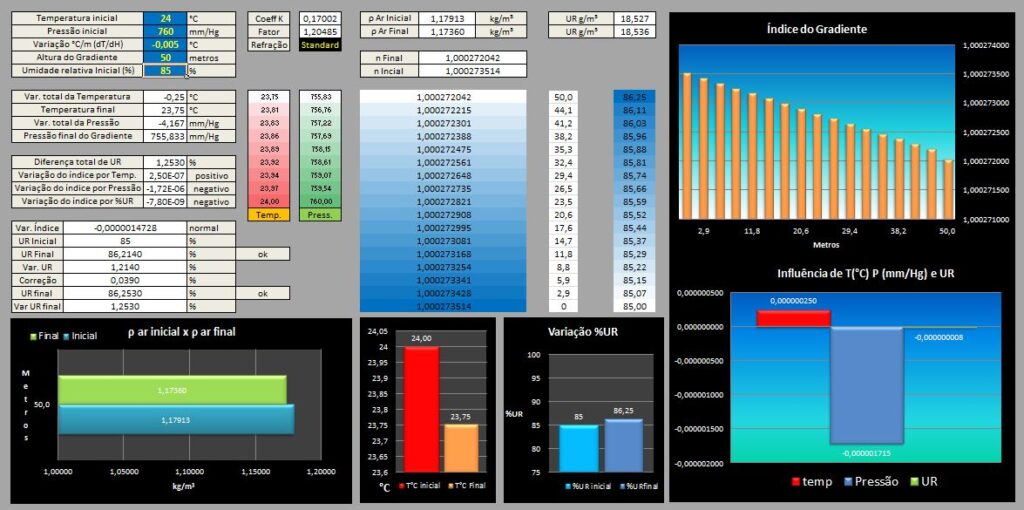
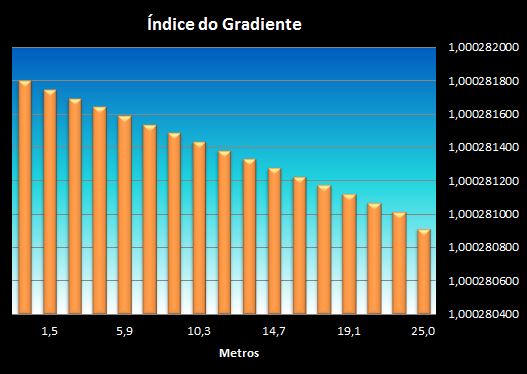
4 Construção do gradiente em função das variações de índice de refração:
A primeira etapa é a definição da pressão, temperatura, UR inicial e a altura final (metros).
Começaremos com 760 mm/Hg , 22°C , 70% de UR e 25 metros.
Tendo como referência o valor de n= 1,0003 15°C 760 mm/Hg ar seco, faremos a primeira correção para obter o índice inicial:
- Alteração por pressão inicial 760 mm/Hg = 0
- Alteração por temperatura: (22°C-15°C)= -7 x 10-6
- Alteração por UR inicial: (70% , 22°C)= -(70 x (var7°C x 2,285 x 10-8))
- Valor inicial: n= 1,0002818
Agora iremos calcular o valor da URmax (g/m3 ) para 20°c e UR 70%:
(%UR÷100)×1330×e^((17,62×T°C)/(T°C+243,12))/((T°C+273,16))
para Ar 22°C URmax = 19,4 g/m3 UR70% = 13,6 g/m3 (UA em 70%)
Esse valor será a referência para o cálculo de variação percentual da UR no gradiente.
Para se obter a variação do índice no gradiente, um dado crucial é a variação de °C/m (dT/dH). Em termos gerais o esperado é uma redução de -6,5°C/km, o que nos dá uma variação de -0,0065°C/m.
Obviamente esse valor se altera, e faremos exemplos diversos, inclusive com inversão térmica.
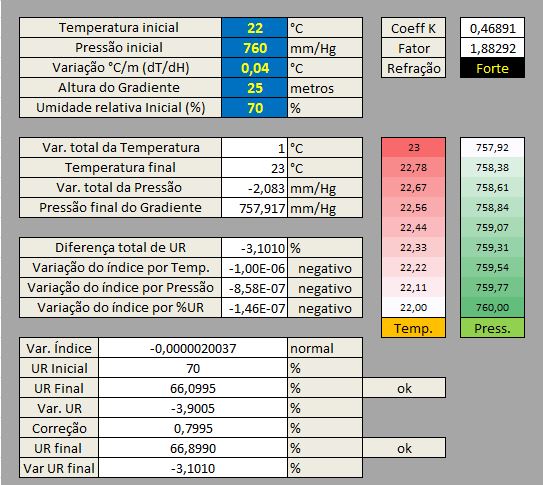
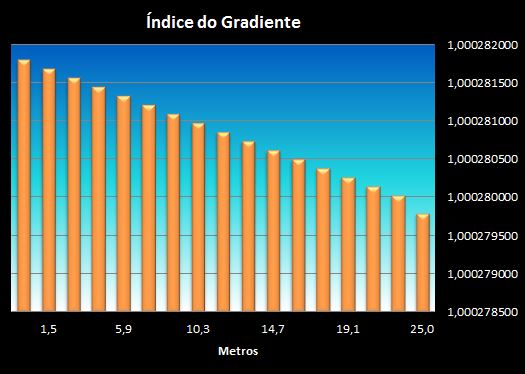
4.1 Refração Forte (k>0,38 a k<0,58)
Uma refração forte indica uma inversão térmica mais intensa, superior a 0,025°C/m ou seja, o ar ao se afastar do solo está ganhando temperatura. Assim como veremos logo adiante, o gradiente adiabático normal (seco ou úmido) possui certos limites para perda de temperatura. O gradiente adiabático inverso também possui limitações muito similares, porém inversas, e sua ocorrência é um pouco mais rara.
4.2 Refração média (k>0,18 a k<0,38)
Uma refração média (≈ K 0,20) ocorre quando a variação dT/dH é muito pequena (± 0,001) e neste caso a variação do índice está ocorrendo somente em função da variação da pressão. Valores positivos >+0,005 já aumentam rapidamente o coeficiente K.
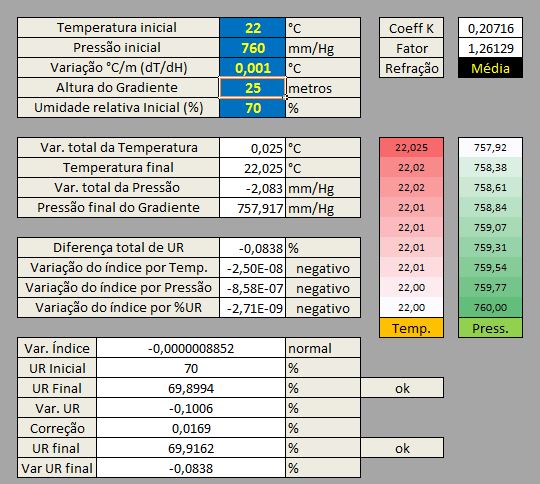

4.2.1 Elevação do Coeficiente ≈ k 0,30
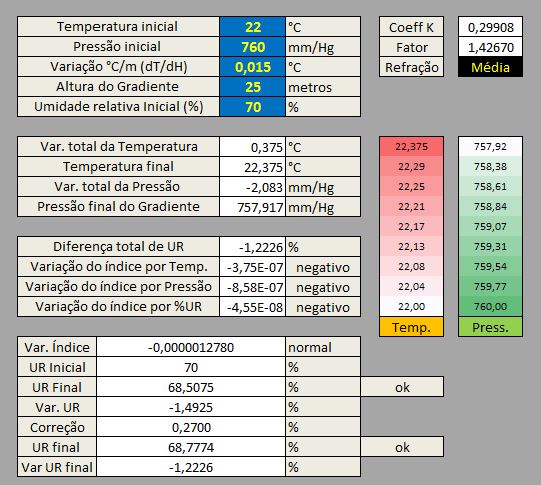
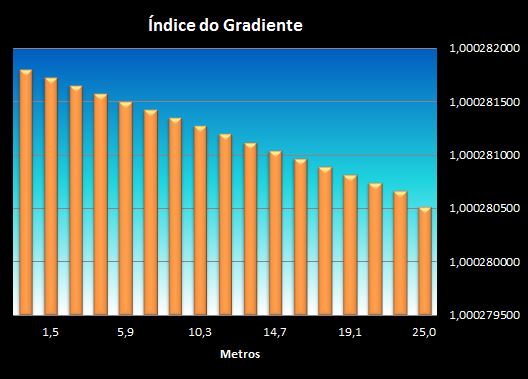
Com o aumento da variação da temperatura dT/dH para 0,015°C/ metro já encontramos um valor de ≈k 0,30
4.3 Refração Standard: (K>0,12 a K<0,18)
Com variações de dT/dH consideradas padrão (-0,01°C/m a -0,0065°C/m) encontramos valores de k dentro da média da refração Standard
4.3.1 Variação de -0,0065°C/m
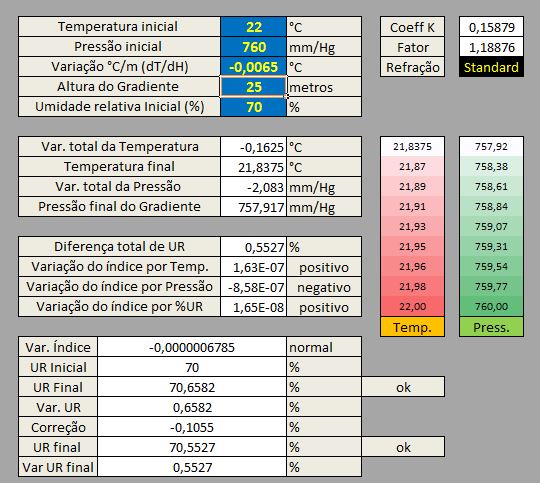
Nota sobre variação e correção de UR: O incremento de 0,6582 % de UR (onde 13,6 g/m3 representam 70,6582% de UR para a temperatura final de 21,8375 °C) está assumindo uma distribuição homogênea da UA (da UR inicial) dentro do gradiente. Para uma depuração dos resultados deve-se utilizar a correção de dispersão, caso contrário, o valor de K em algumas situações, assume um valor maior do que o real:
Diferença%UR + ( Htotal (4,7 x (dT/dH)) ) , o que e garante maior precisão quando obtemos dados de temperatura, UR e variação de °C/m em campo . Assim obtemos o valor corrigido de 0,5527%
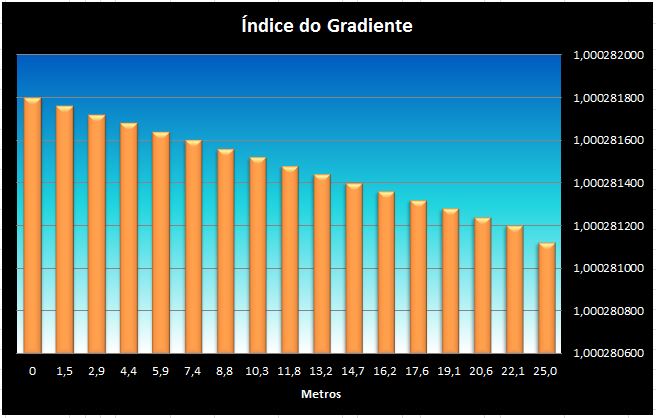
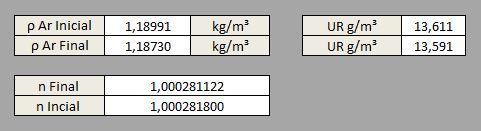
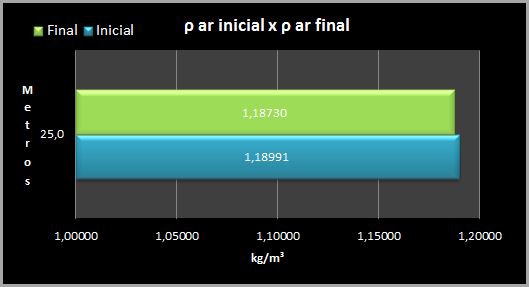
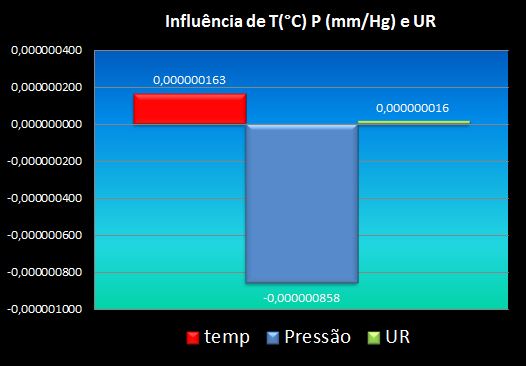
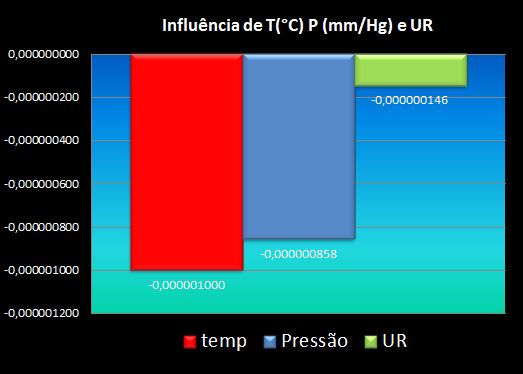
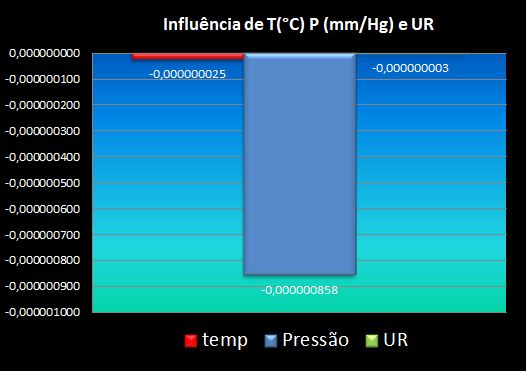
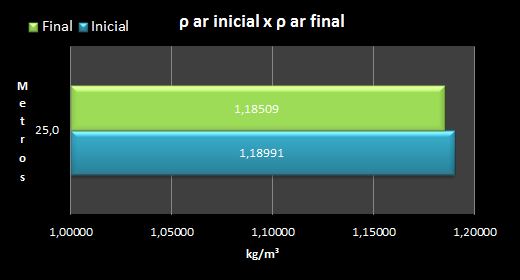
Nota-se claramente que a maior influência na variação do índice se deve à diminuição da pressão, sobrepondo-se ao ganho de índice por temperatura e variação percentual de UR.
4.3.2 Variação de -0,01°C/m:
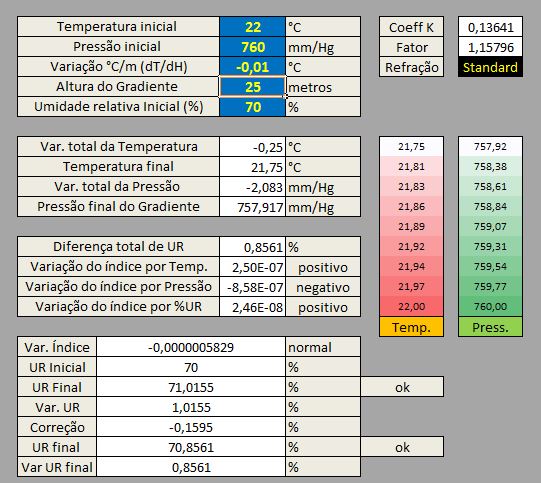
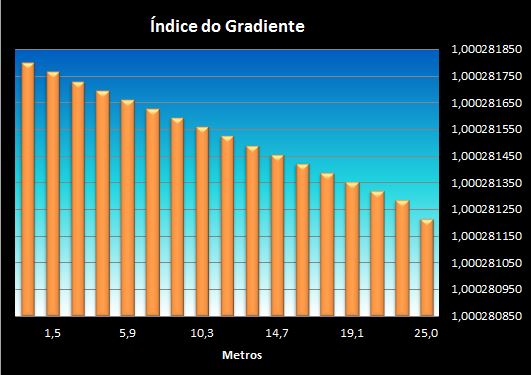
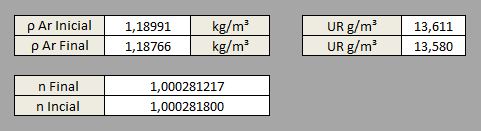
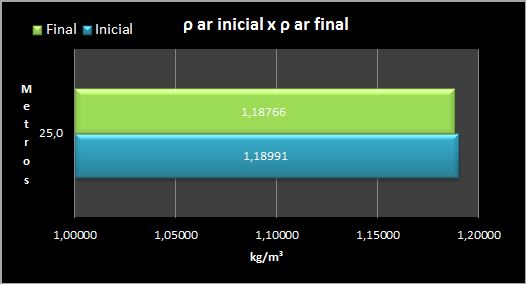
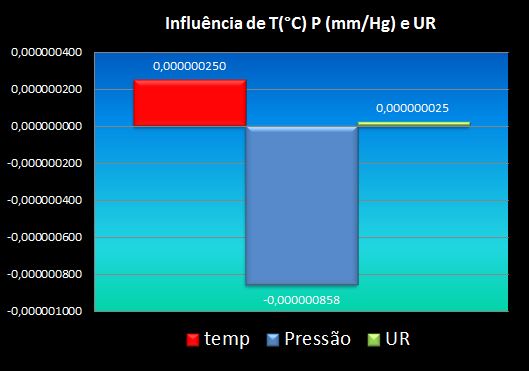
A variação por pressão, ainda se sobrepõe, evidenciando que será necessária uma diminuição mais severa da temperatura para que o K se aproxime de zero (onde a refração é quase nula) e inicie a estabilização.
4.4 Estabilização do gradiente (K=0):
Agora aplicaremos um valor de -0,0317°C/m lembrando que uma variação dessa ordem não se aplica em grandes extensões de altura, já que teríamos -31,7°C/km. Variações com taxa superior a +- 0,025°C/m normalmente se estendem por algumas centenas de metros e tendem a uma redução gradativa com ganho de maior elevação e ocorrem com maior facilidade em terrenos elevados ou com geografia mais irregular com elevações e depressões significativas em pouca extensão de terreno. Lembrando que a referência de faixa “standard” do coeficiente k segue o gradiente adiabático “seco” (Ar não saturado) é de -0,01°C/m ou -10°C/km e quando já existe a condensação é considerado “úmido” e sua variação é na ordem de -0,005°C/m ou -5°C/km.
O exemplo a seguir mostra a refração se aproximando de K=0
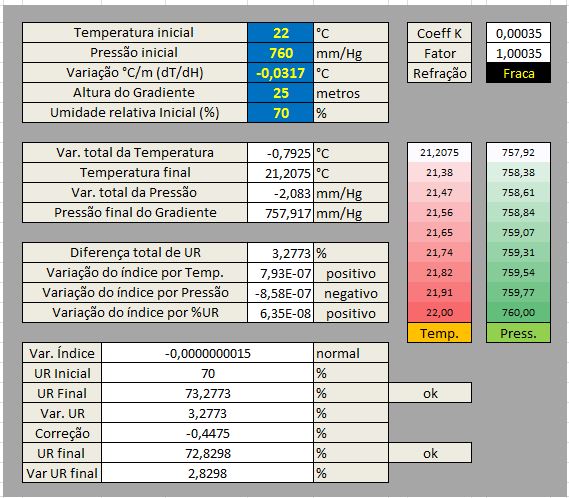
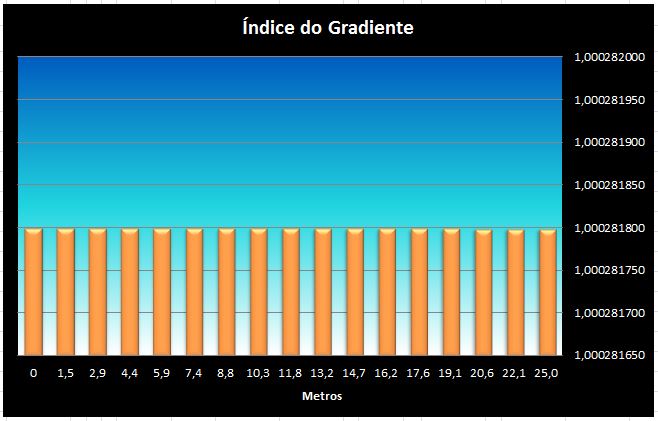
Nessa condição, a variação de índice dentro do gradiente é praticamente nula, portanto não existem desvios significativos. (Refração fraca ou muito fraca).
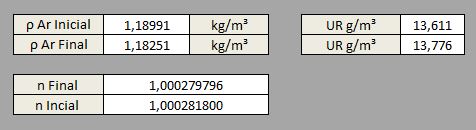
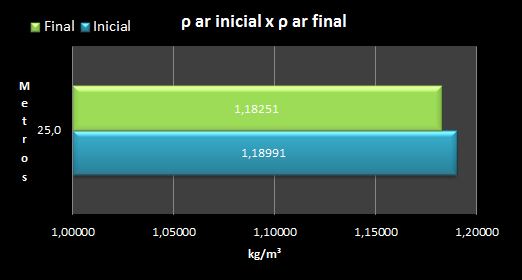
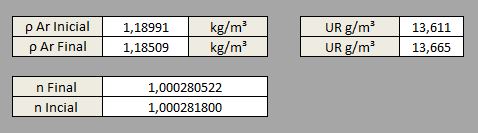
Outro ponto importante é a observação da densidade inicial e final do ar que, como o esperado, está muito próxima do equilíbrio:
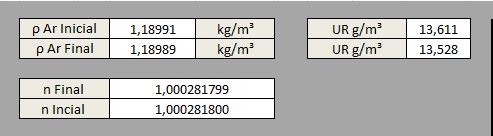
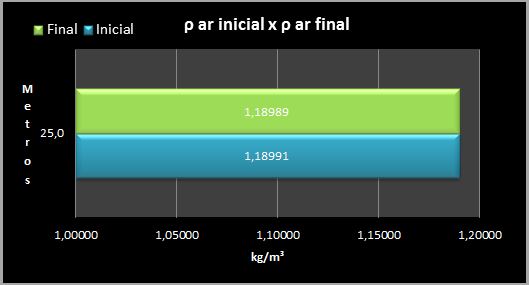
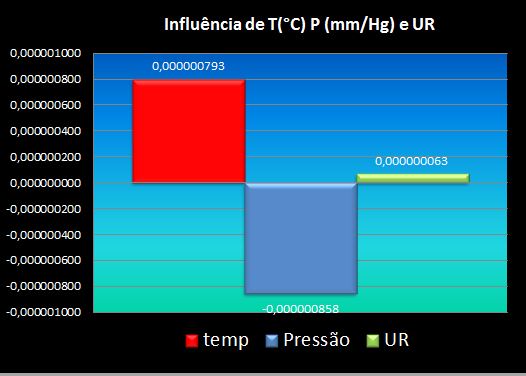
4.5 Início e limite de inversão:
Abaixo de -0,032°C/m já inicia-se a inversão ( K= -0,0015) porém a diferença de densidade ultrapassa o ponto de estabilidade em -0,034°C/m na extensão de 15 metros.
Lembrando que a referência do coeficiente K é utilizada em situações atmosféricas sustentáveis e não para gradientes complexos e compostos onde podem se formar efeitos atmosféricos de reflexão total inferior, superior, reflexões múltiplas, entre outros.
Mas daremos alguns exemplos para explanação.
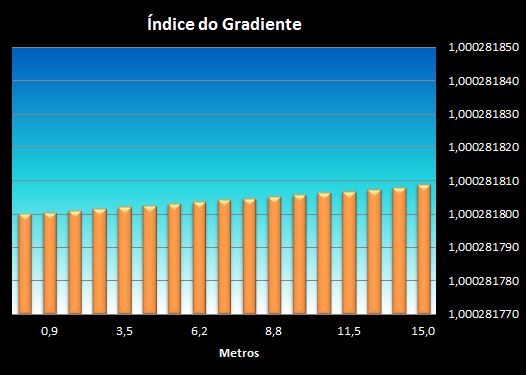
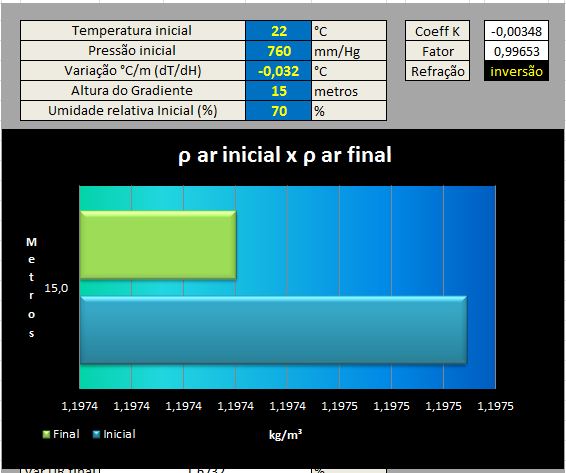
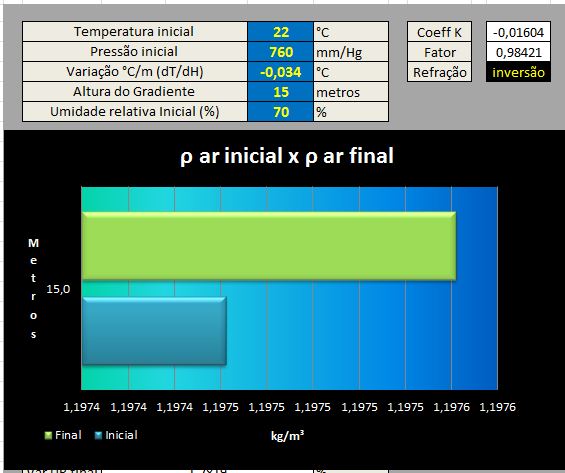
4.5.1 Aumento da Inversão
Para o valor de inversão aumentar ( valores que tendem a K = -1) é necessário maior variação térmica, UR inicial menor e gradientes de menor altura. Assim a convergência do ar nas áreas próximas consegue gerar mais sustentação para a camada mais densa, suprindo a falta de empuxo (consequência da diferença de densidade) através do movimento de convecção térmica dentro da faixa de inversão mais severa do gradiente que normalmente possui pouca altura. Também pode ocorrer variações inferiores a k -1, com variações muito acentuadas de temperatura, as quais normalmente se formam muito próximas ao solo (ou qualquer outra fonte térmica) e isso é o que ocasiona a maioria das miragens inferiores, por exemplo.

É importante entender que variações térmicas (dT/dH) mais intensas, tanto negativas como positivas, são melhores compreendidas da seguinte forma: a fonte térmica ( entenda-se como “solo”, água, gelo, areia, etc.) é a principal responsável pela irradiação térmica em questão, já que partimos de uma altura de “zero metros”( Referência de base para 760 mm/Hg, mas pode-se alterar a pressão inicial e utilizar o “zero” para construção do gradiente em relação ao solo em qualquer altimetria). O ar perde e ganha temperatura rapidamente, portanto essa variação está atrelada à curtas distâncias da fonte térmica em questão.
Agora utilizaremos uma variação de -0,14°C/m e faremos o K se aproximar de K= -1 com 25°C iniciais e 45%UR em 1 metro.
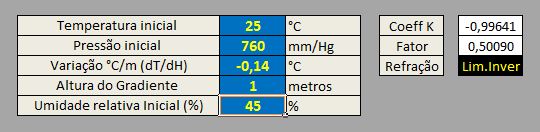
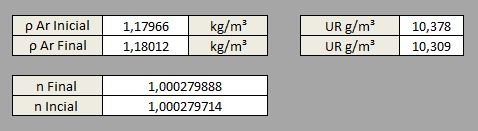
A variação da densidade já ultrapassou o ponto de estabilidade porém ainda é uma situação possível, devido à pequena altura e provável sustentação por convecção.
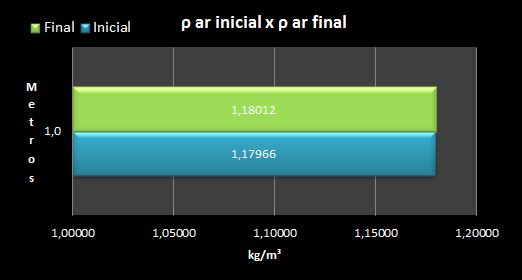
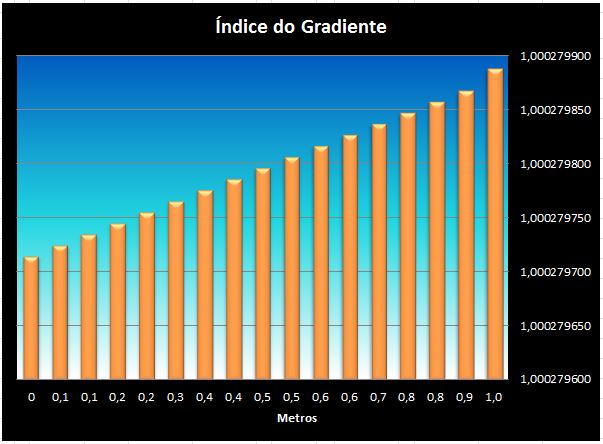
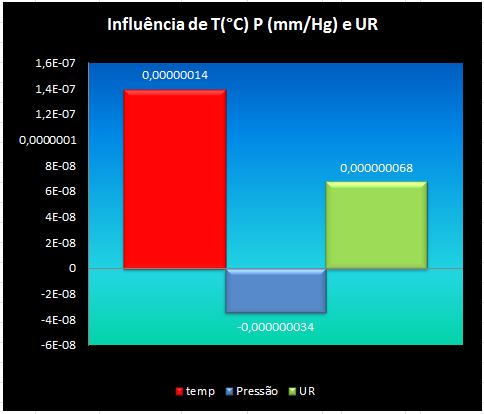
Agora um exemplo para 15 metros mantendo-se os mesmos 25°C:
Essa situação é sustentável somente em uma pequena fração de altura (exemplo anterior) justamente pela rápida alteração da densidade.
Assim como o valor de K também já não se encontra mais no limite de inversão.
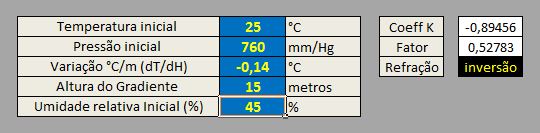
A variação da densidade não é sustentável:

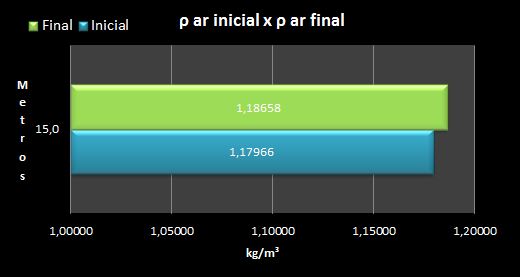
Basicamente quanto mais severa é variação dT/dH °C/m, menor é a altura sustentável da inversão do gradiente.
Ou seja, as “inversões” de gradiente somente se sustentam por pequenos intervalos de altura. As variações de temperatura necessárias para “atmosfera de gradiente inverso” não são fisicamente tangíveis, uma vez que a “inversão da densidade” não pode ser aplicada indefinidamente.
Conclusão
Os resultados obtidos através do cruzamento de dados entre os fatores que influenciam a variação do índice de refração do ar atmosférico e o comportamento esperado das variações atmosféricas como mudança de temperatura em função da altura, variação de pressão, gradientes adiabáticos e variação de umidade relativa, produzem valores absolutamente coerentes ao coeficiente k utilizado nas correções durante observações em campo, onde este referido valor é imprescindível para a obtenção de resultados corretos em medições topográficas, geodésicas, astronomia de posição, entre outros.
Referências Bibliográficas
- https://en.wikipedia.org/wiki/Density_of_air
- http://user.engineering.uiowa.edu/~ece195/2006/docs/RefractionAttenuation.pdf
- https://geodaesie.info/sites/default/files/privat/zfv_2012_3_Reiterer.pdf
- https://www.researchgate.net/publication/228937337_Monitoring_of_the_refraction_coefficient_in_the_lower_atmosphere_using_a_controlled_set-up_of_simultaneous_reciprocal_vertical_angle_measurements/link/00b495292e9d80f8cf000000/download
- https://www.tec-science.com/mechanics/gases-and-liquids/barometric-formula-for-an-adiabatic-atmosphere/#:~:text=Therefore%2C%20in%20the%20atmosphere%20assumed,decrease%20in%20temperature%20is%20obtained.&text=Assuming%20an%20adiabatic%20atmosphere%2C%20the,dry%20adiabatic%20lapse%20rate)!
- https://drive.google.com/file/d/14VgEfibuER3lwHUbEjgziXfH_4S6GFAv/view?usp=sharing
- https://en.wikipedia.org/wiki/Nitrogen
- http://web.archive.org/web/20200517215848/http://walter.bislins.ch/bloge/index.asp?page=Deriving+Equations+for+Atmospheric+Refraction
- http://walter.bislins.ch/bloge/index.asp?page=Advanced+Earth+Curvature+Calculator
- http://web.archive.org/web/20200516203645/https://www.engineeringtoolbox.com/humidity-ratio-air-d_686.html
- https://www.researchgate.net/publication/328049550_Determinando_a_umidade_absoluta_do_ar_a_partir_da_umidade_relativa
- https://repositorio.ufpb.br/jspui/bitstream/tede/8004/2/arquivo%20total.pdf
